Bài 11: Functor
Functor
Đến giờ, ta đã gặp nhiều class trong thư viện chuẩn, bao gồm Ord, với Eq, với Show, với Read. Và bây giờ, ta xét đến Functor, về cơ bản là những thứ có thể được map.
Functor được định nghĩa như sau:
class Functor f where
fmap :: (a -> b) -> f a -> f b
Ta thấy rằng nó định nghĩa một hàm, fmap, và không cho ta bất kì cách thực thi mặc định nào cho nó. Kiểu fmap rất thú vị vì trong số các định nghĩa typeclass đã gặp , tham số kiểu đóng vai trò là kiểu trong class luôn là kiểu cụ thể, như a trong (==) :: (Eq a) => a -> a -> Bool. Nhưng giờ đây, f không phải là kiểu cụ thể (như Int, Bool hoặc Maybe String), mà là một type constructor nhận vào một tham số kiểu. Một ví dụ nhanh chóng để ôn lại: Maybe Int là kiểu cụ thể, còn Maybe là type constructor chỉ nhận vào kiểu với vai trò tham số. Dù sao thì ta thấy rằng fmap nhận vào một hàm ánh xạ từ a sang b và functor áp dụng trên a rồi trả về functor áp dụng trên b.
Đừng lo nếu diều này nghe có vẻ dễ nhầm lẫn. Tất cả sẽ sớm được sáng tỏ khi điểm qua một vài ví dụ. Type signature của map là map :: (a -> b) -> [a] -> [b], trong trường hợp bạn không biết. Nó cũng nhận vào hàm ánh xạ từ a sang b và List kiểu a, rồi trả về List kiểu b, như vậy map chính là fmap được cụ thể hóa trên List. Đây là cách để khai báo List là thể hiện của Functor.
instance Functor [] where
fmap = map
Như vậy đó! Lưu ý rằng ta không code instance Functor [a] where, vì từ fmap :: (a -> b) -> f a -> f b, ta thấy được rằng f phải là type constructor, nhận vào kiểu. [a] là một kiểu cụ thể (List kiểu a), còn [] là một type constructor nhận vào kiểu và tạo ra kiểu cụ thể như [Int], [String] hoặc thậm chí [[String]]. Đối với List, fmap chỉ đơn thuần là map nên ta nhận kết quả hệt như vậy khi dùng chúng với List.
map :: (a -> b) -> [a] -> [b]
ghci> fmap (*2) [1..3]
[2,4,6]
ghci> map (*2) [1..3]
[2,4,6]
Khi ta map hoặc fmap lên List rỗng, dĩ nhiên sẽ thu được List rỗng. Chỉ có điều List rỗng kiểu [a] biến thành List rỗng kiểu [b].
Những kiểu dữ liệu nào đóng vai trò như cái hộp thì có thể thành functor.
Bạn có thể hình dung List là một cái tủ có vô vàn những ngăn nhỏ và mỗi ngăn có thể trống rỗng hoặc đầy. Như vậy, ở mỗi ngăn có thuộc tính kiểu Maybe a. Ở một chừng mực nào đó, cũng giống như một cái hộp có thể không chứa gì, tương ứng với giá trị Nothing, hoặc chỉ chứa “HAHA”, tương ứng với giá trị Just "HAHA". Sau đây là cách mà Maybe đóng vai trò functor.
instance Functor Maybe where
fmap f (Just x) = Just (f x)
fmap f Nothing = Nothing
Một lần nữa, hãy chú ý cách sử dụng instance Functor Maybe where thay vì instance Functor (Maybe m) where, cũng như ta đã làm với Maybe và YesNo. Functor cần type constructor nhận vào một kiểu, không phải kiểu cụ thể. Nếu thử tưởng tượng việc thay thế f bằng Maybe thì fmap sẽ là (a -> b) -> Maybe a -> Maybe b và cách này có vẻ ổn. Nhưng nếu bạn thay thế f bằng Maybe m thì nó sẽ là (a -> b) -> Maybe m a -> Maybe m b, tức là chẳng có ý nghĩa gì bởi Maybe chỉ nhận duy nhất một tham số kiểu.
Dù sao đi nữa, fmap khá đơn giản. Nếu nó là rỗng: Nothing, thì chỉ cần trả về Nothing (nếu ta map trên ngăn rỗng thì ta thu được ngăn rỗng). Cũng như ta map trên List ngăn, ta sẽ nhận được List ngăn. Nếu nó không ngăn, mà là giá trị đơn lẻ đặt trong Just, thì ta áp dụng hàm đối với nội dung của Just.
ghci> fmap (++ "ABC") Nothing
Nothing
ghci> fmap (*2) (Just 200)
Just 400
ghci> fmap (*2) Nothing
Nothing
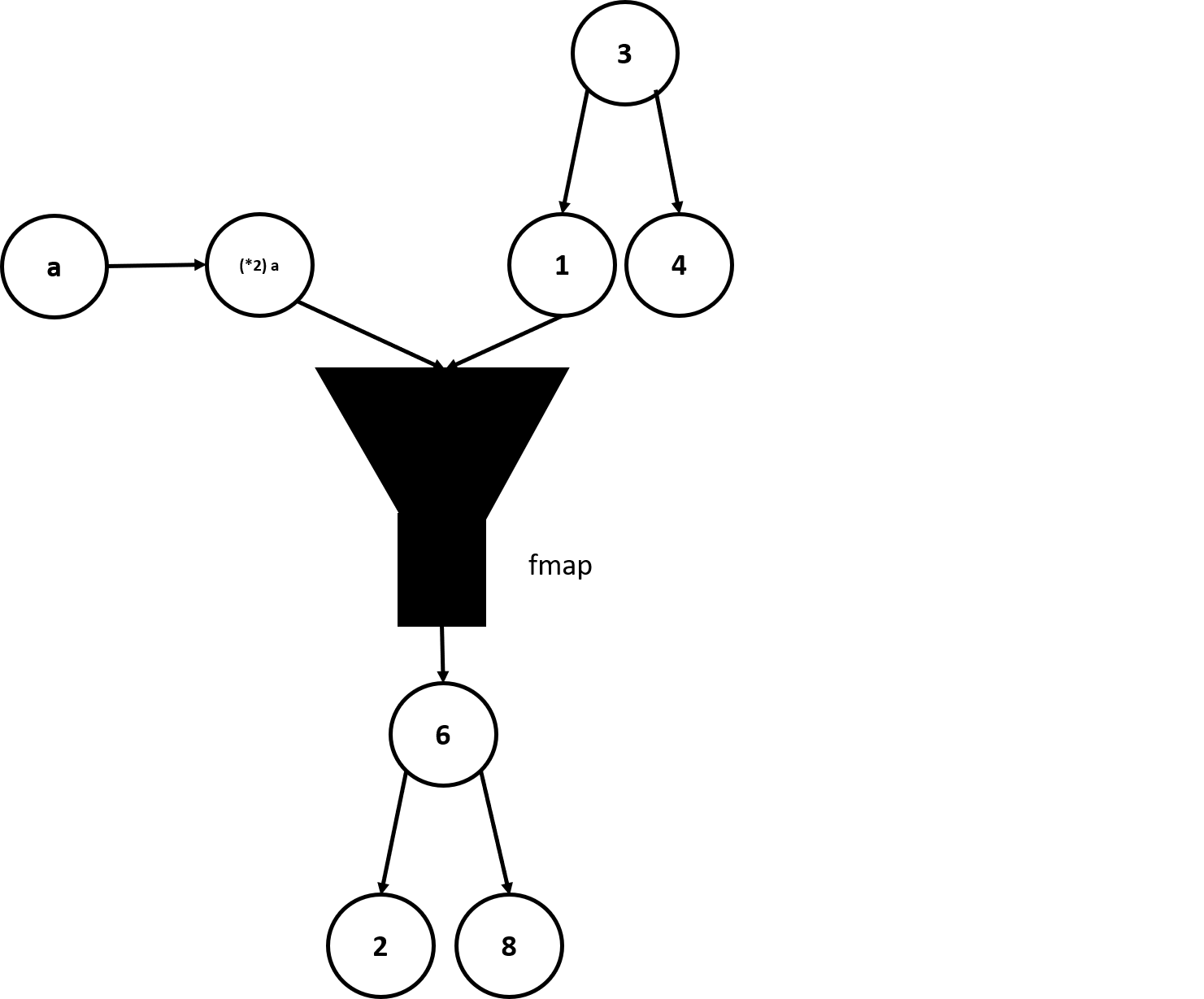
Một thể hiện khác của Functor chính là BST. Nó có thể được hình dung như một cái hộp (theo khía cạnh có thể giữ nhiều giá trị hoặc không giữ thứ gì) và type constructor Tree nhận vào đúng một tham số kiểu. Nếu bạn xét fmap như thể nó là một hàm để dành riêng cho Tree thì type signature của nó sẽ là (a -> b) -> Tree a -> Tree b. Ta sẽ dùng đệ quy đối với kiểu dữ liệu này. Map trên cây rỗng sẽ tạo ra cây rỗng, map trên cây không rỗng sẽ tạo ra một cây trong đó hàm được áp dụng cho gốc, còn cây con trái và phải được đệ quy tiếp.
instance Functor Tree where
fmap f EmptyTree = EmptyTree
fmap f (Node x leftsub rightsub) = Node (f x) (fmap f leftsub) (fmap f rightsub)
ghci> fmap (*2) EmptyTree
EmptyTree
ghci> fmap (*4) (foldr treeInsert EmptyTree [5,7,3,2,1,7])
Node 28 (Node 4 EmptyTree (Node 8 EmptyTree (Node 12 EmptyTree (Node 20 EmptyTree EmptyTree)))) EmptyTree
Với Either a b ta có đôi chút vấn đề, functor chỉ nhận một tham số kiểu nhưng Either lại nhận hai tham số nên chúng ta phải áp dụng Either từng phần bằng cách chỉ cấp cho nó một tham số và còn một tham số tự do. Đây là cách làm cho Either là functor trong thư viện chuẩn:
instance Functor (Either a) where
fmap f (Right x) = Right (f x)
fmap f (Left x) = Left x
Dễ thấy rằng chúng ta để Either a thành một thể hiện thay vì Either. Đó là vì Either a là nhận vào một tham số, trong khi Either thì nhận vào hai tham số. fmap trên Either a sẽ là (b -> c) -> Either a b -> Either a c (hay (b -> c) -> (Either a) b -> (Either a) c). Trong đoạn code trên, ta đã map trong trường hợp có type constructor là Right, nhưng lại không map trong trường hợp Left. Nếu nhìn trở lại cách định nghĩa Either a b, ta sẽ thấy nó có dạng:
data Either a b = Left a | Right b
Như vậy, nếu ta muốn map một hàm lên cả hai vế, thì a và b phải cùng kiểu. Ví dụ, nếu ta thử map hàm nhận và trả về String trong khi b là String mà a lại là Num thì sẽ hơi vô lý. Hơn nữa, từ việc thấy được kiểu của fmap sẽ là gì khi nó chỉ hoạt động với các giá trị Either, ta thấy rằng tham số thứ nhất phải giữ nguyên còn tham số thứ hai có thể thay đổi được; và tham số thứ nhất thực tế là constructor value Left.
Map trong Data.Map cũng có thể thành functor vì chúng giữ giá trị (hoặc không giữ thứ gì!). Trong trường hợp Map k v, fmap sẽ map một hàm v -> v' trên Map k v rồi trả về Map k v'.
Lưu ý rằng dấu ' thường dùng để chỉ những thứ gần giống nhau, chỉ thay đổi chút ít.
Hãy cố gắng tự hình dung xem bằng cách nào mà ta có thể làm cho Map k trở thành thể hiện của Functor!
instance (Ord k) => Functor (Map k) where
fmap f m = fromList (map modify (toList m)) where modify (k,v) = (k, f v)
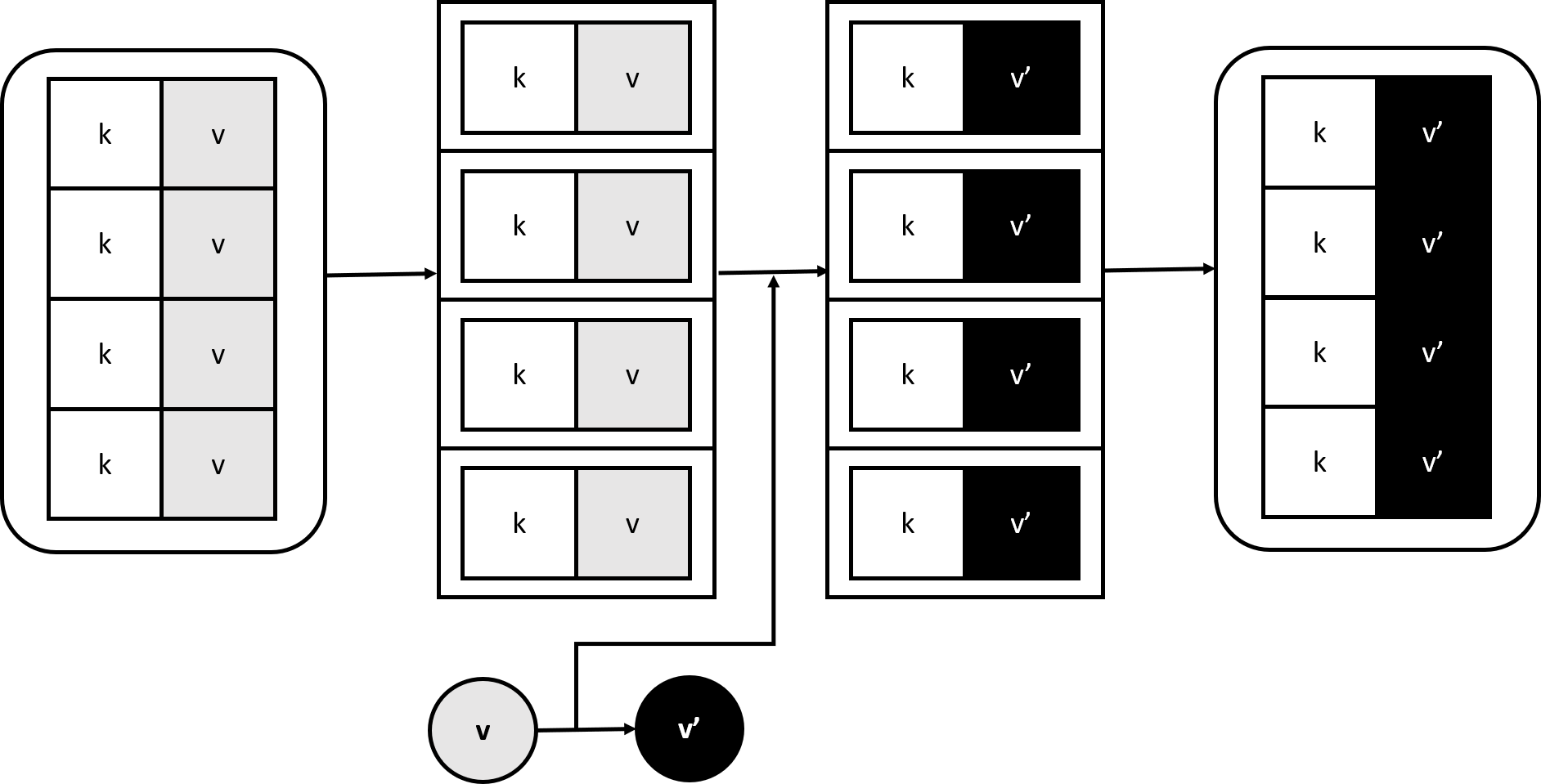
Trường hợp này khá phức tạp khi ta phải chuyển đổi qua lại giữa Map và List. Đầu tiên ta phải ép phẳng Map về List các tuple bằng hàm toList, sau đó map hàm modify lên List mới (modify là hàm nhận vào một tuple, sau đó thay đổi phần tử thứ hai trong tuple đó). Cuối cùng chuyển List ngược về Map. Nếu f :: a -> b thì có thể thấy rằng key k trong Map k v vẫn được bảo toàn, còn v vốn có kiểu a đã được biến đổi thành v' kiểu b bằng f. Rốt cuộc fmap :: f -> (Map k v) -> (Map k v)`.
Với functor, ta đã mô tả được một hành vi cấp cao khá hay.
Còn một điều nữa! Functor cần tuân theo một số định luật để chúng có những thuộc tính mặc định. Ví dụ fmap (+1) [1,2,3,4] sẽ trả về [2,3,4,5] chứ không phải ngược lại, [5,4,3,2]. Nếu ta dùng fmap (\a -> a) (hàm đồng nhất) đối với một List nào đó, ta sẽ nhận về đúng List ban đầu. Chẳng hạn, fmap đối trên BST tạo nên cây mới nhưng tính chất cây phải lớn hơn cây trái vẫn phải đảm bảo. Trong chương sau ta sẽ đề cập chi tiết đến các định luật áp dụng cho functor.