Bài 01: Haskell căn bản
Những kiến thức căn bản bạn cần biết về Haskell.
1.0. Lời tựa
Hình 1.0.1. Logo Haskell, lấy cảm hứng từ Monad >>= (một khái niệm trừu tượng trong Haskell) và Lambda λλ (chữ cái Hy Lạp)
Tôi quyết định viết những trang blog này vì muốn học lại kiến thức về Haskell (theo phương pháp của Feynman) và trong tương lai gần, khi lập trình hàm lên ngôi, tôi mong mình có thể giúp những người chưa biết gì về Haskell học tư duy của ngôn ngữ này nhanh chóng. Cho đến hiện tại, hầu như không có hướng dẫn chuẩn nào trên mạng (đặc biệt là tiếng việt), đa số chỉ là những blog lẻ tẻ. Khi bắt đầu học Haskell, học từ một nguồn tài liệu duy nhất là không đủ, cách học của tôi là đọc vài cuốn sách khác nhau, bài báo khoa học nữa, vì mỗi tài liệu đều có cách diễn giải riêng.
Hình 1.2. Một số nguồn tự học Haskell
Blog này chủ yếu dành cho những người đã có kinh nghiệm với C, C++, Java, Python, … nhưng chưa từng biết đến lập trình hàm (Haskell, ML, OCaml …). Tuy nhiên nếu bạn chưa từng lập trình thì vẫn có thể dễ tiếp thu một cách dễ dàng.
Trước khi hiểu Haskell, tôi đã thất bại nhiều lần vì nó khá dị và đi ngược lại với tư tưởng OOP trước giờ. Nhưng một khi đã “vào guồng”, mọi chuyện sẽ thuận buồm xuôi gió. Học Haskell rất giống với lần đầu học lập trình - rất vui.
1.1. Hướng dẫn đọc
Trong series này sẽ có khá nhiều hình minh họa và ký hiệu liên quan đến toán học, do đó tôi quy ước vài điều như sau:
1.1.1. Ký hiệu
ff, gg, … là hàm, hàm đơn giản là một thực thể nhận đầu vào, xử lý gì đó và trả về kết quả. Ở trong Haskell chúng ta xem mọi thứ đều là hàm, kể cả những giá trị như 5, 100, … (hàm hằng).
aa, bb, … hay những chữ cái thường (hoặc từ có chữ cái đầu thường) đại diện cho tham số (hay giá trị cụ thể) được truyền vào và sử dụng trong thân hàm. Ví dụ: a\=5a\=5, newList\=[1,2,3]newList\=[1,2,3], …
FF, AA, MM, … hay những chữ cái in hoa (hoặc từ có chữ cái đầu in hoa) ký hiệu cho kiểu dữ liệu trừu tượng. Ví dụ: OrdOrd là kiểu dữ liệu có thứ tự, BoolBool là kiểu dữ liệu thuộc về đại số Boolean, ….
1.1.2. Quy ước về hình ảnh minh họa
Tôi sẽ sử dụng hình vuông để ký hiệu cho hàm và hình vuông có cạnh là nét đứt ký hiệu cho phép áp dụng hàm (gọi hàm).
Hình vuông bo tròn ở góc biểu thị cho ngữ cảnh (context) ở các kiểu dữ liệu trừu tượng.
Mũi tên biểu thị cho liên kết giữa các hàm và mũi tên nét đứt biểu diễn thứ tự biến đổi của các đối tượng (trình tự thời gian).
1.2. Haskell là gì?
Hình 1.2.1. Một hàm số cơ bản
Haskell là một ngôn ngữ lập trình hàm thuần túy (purely functional programming language). Nó khác với những ngôn ngữ lập trình bạn đã gặp ở chỗ chúng ta thường giải quyết bài toán bằng cách đặt ra một loạt các bước làm thay đổi trạng thái của các biến trong chương trình. Chẳng hạn, gán a = 5 là giá trị khởi điểm, rồi gán lại một giá trị khác hoặc xài for, while do, … Chương trình giống như một cái máy, ta yêu cầu chúng lặp đi lặp lại công việc nào đó. Trong lập trình hàm, lập trình viên chỉ cần nói cho máy tính biết cần phải làm điều gì thông qua định nghĩa hàm. Ví dụ, n!n! là tích các số nguyên từ 1 đến n, ∑mi\=0xi∑i\=0mxi là x0+∑mi\=1xix0+∑i\=1mxi và cứ như vậy cho đến khi i\=mi\=m. Bạn có thể tưởng tượng lập trình hàm giống như chúng ta giải quyết bài toán theo cách ngắn gọn nhất bằng cách sử dụng các định nghĩa, định lý, phép biến đổi, …
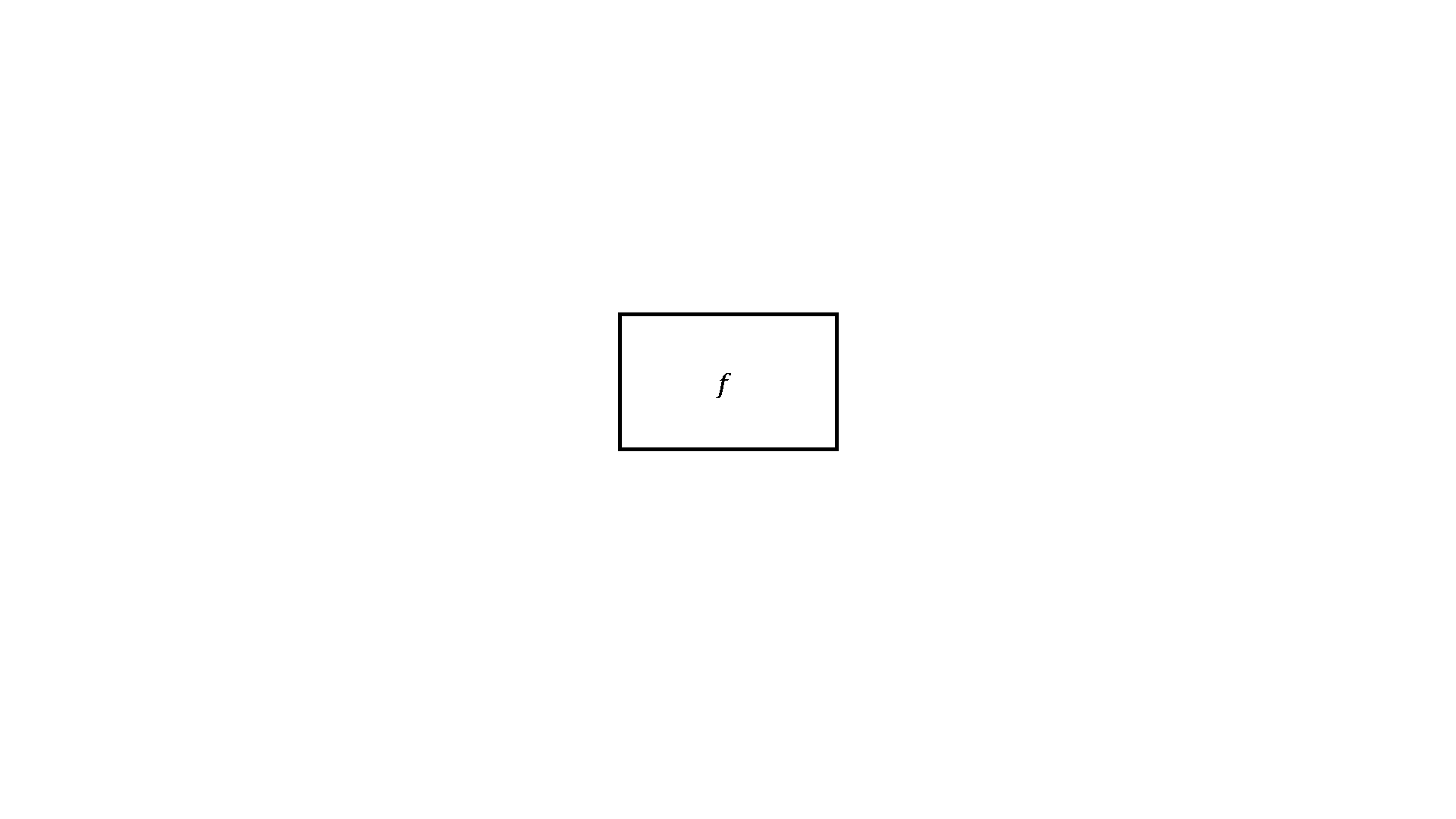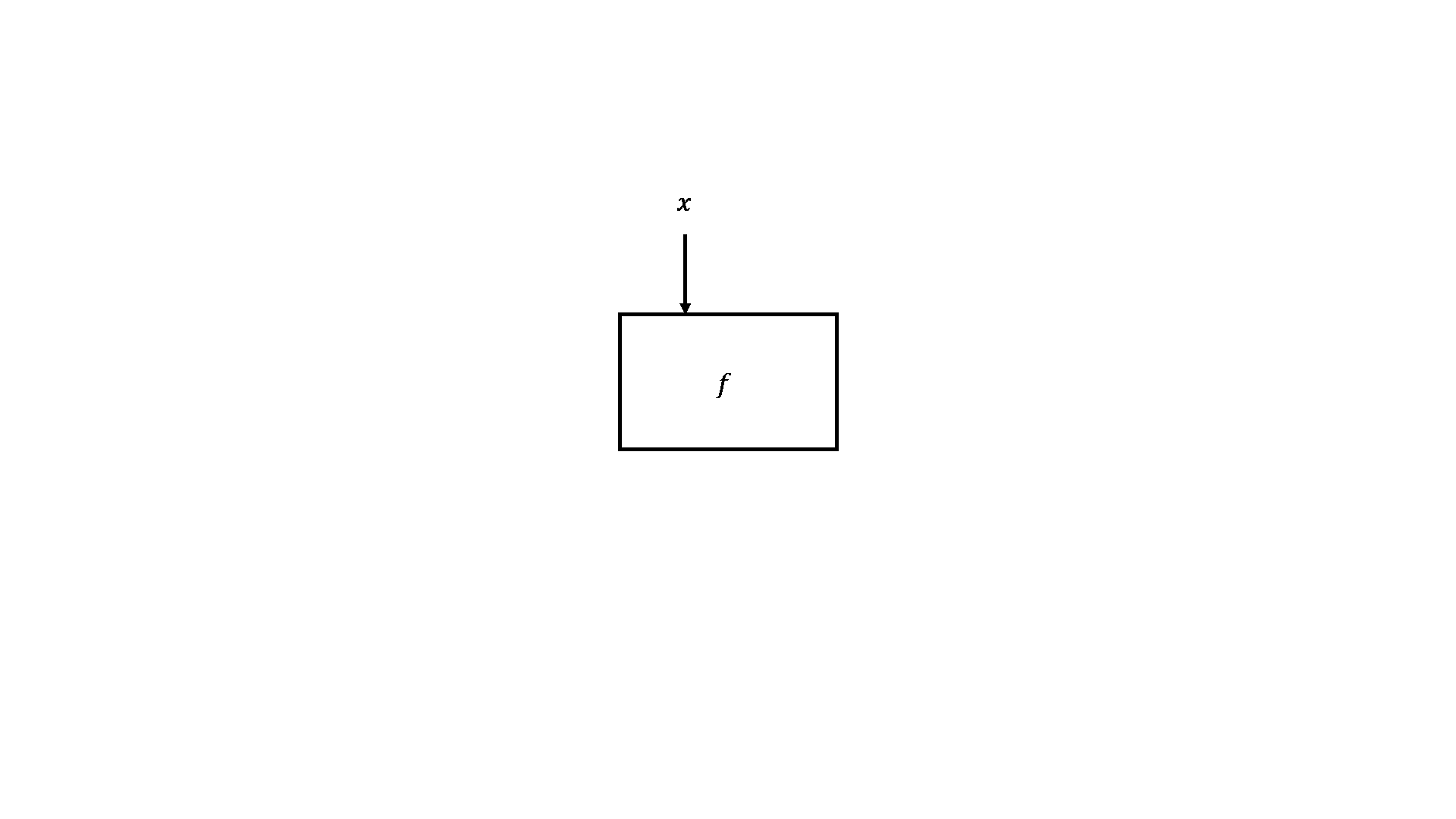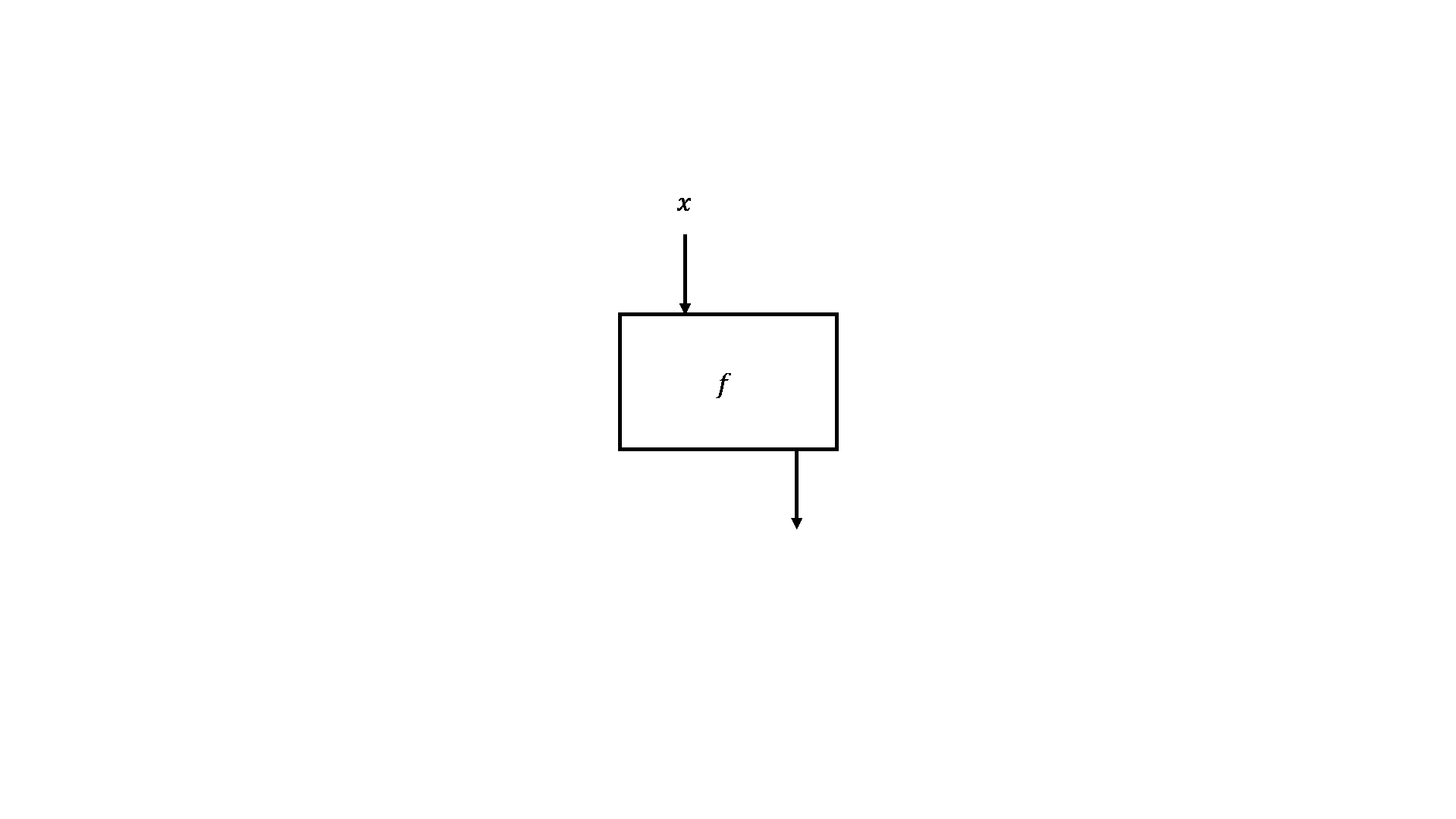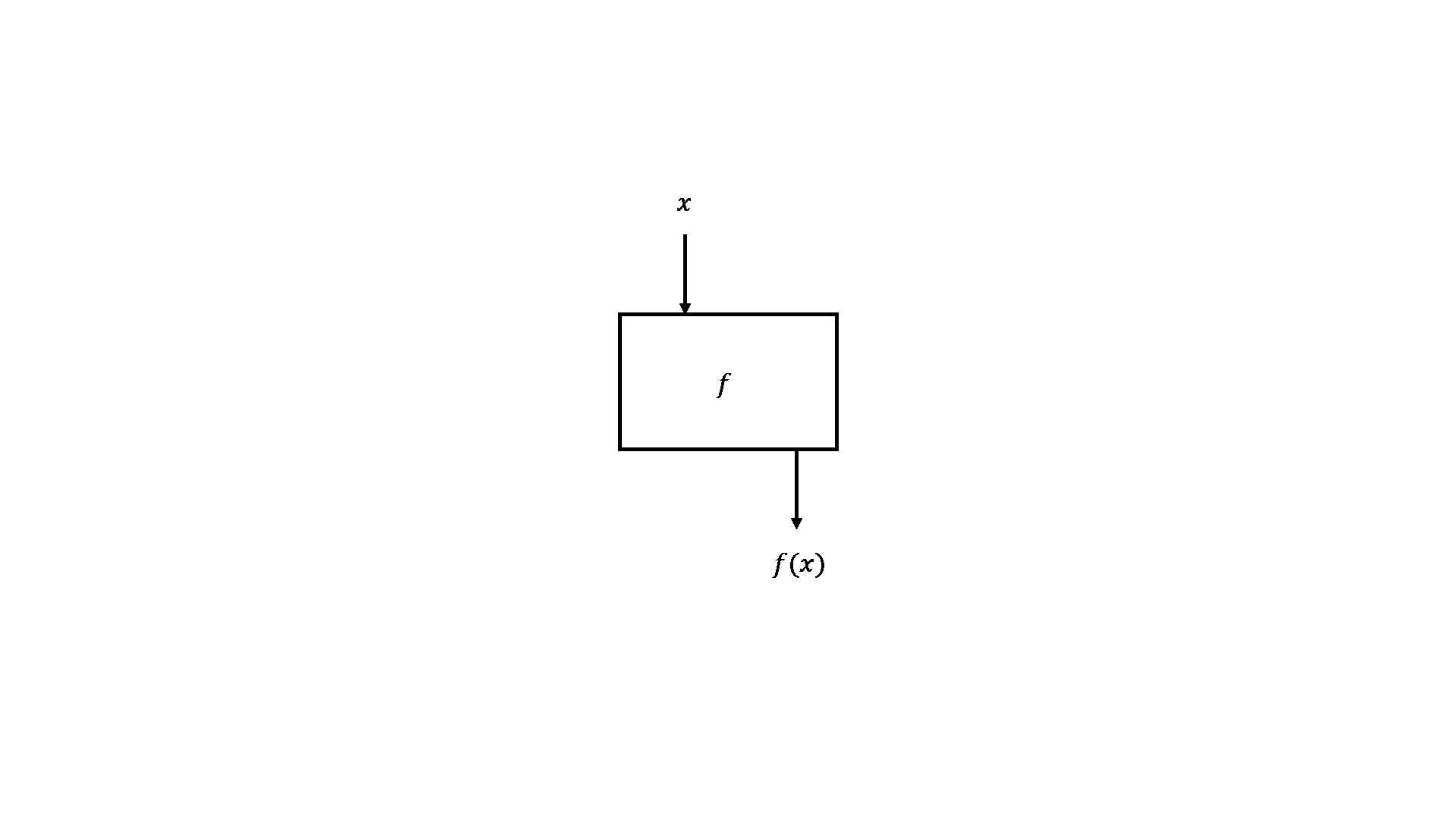Hình 1.2.2. Vòng đời của một hàm, nhận tham số, xử lý và trả về kết quả
Việc gán a = 5, rồi lại thay đổi giá trị của nó được gọi hiệu ứng lề (side effect), vốn đã quá quen thuộc trong quá trình chúng ta lập trình, tuy nhiên Haskell đã loại bỏ hoàn toàn chúng bằng cách định nghĩa mọi thứ bằng hàm. Điều duy nhất hàm thực hiện là lấy tham số (1), tính toán (2) và trả lại giá trị (3). Thoạt đầu, điều này có vẻ tù túng nhưng về sau chúng ta sẽ nhận ra lợi ích của nó. Thứ nhất, nếu một hàm được gọi nhiều lần với cùng tham số thì nó luôn luôn trả về cùng kết quả, tính chất này được gọi là minh bạch tham chiếu (referential transparency) và cho phép trình biên dịch hiểu được hành vi của chương trình. Thứ hai, nó giúp bạn suy luận (thậm chí chứng minh) rằng hàm đó đúng, để từ đó xây dựng những hàm phức tạp hơn bằng cách kết hợp những hàm đơn giản lại.
Lazy
Haskell có tính lười (lazy). Tức là trừ khi đưa ra yêu cầu cụ thể thì Haskell sẽ không thực thi cho đến khi nó thực sự phải trả về kết quả. Đặc tính này kết hợp tốt với referential transparency, giúp cho chúng ta hình dung chương trình như là một loạt những phép biến đổi (transformation). Hay cho phép tồn tại những điều thú vị như cấu trúc dữ liệu vô hạn. Giả sử bạn có List xs = [1,2,3,4,5,6,7,8] và hàm doubleMe có nhiệm vụ nhân mỗi phần tử lên 2 lần rồi trả lại một List mới. Nếu ta muốn nhân List này lên 8 lần, bằng cách dùng ngôn ngữ lập trình khác như C và viết doubleMe(doubleMe(doubleMe(xs))), thì nó sẽ duyệt qua List một lần để tạo một bản sao (tempt) rồi trả lại List, sau đó làm tương tự hai lần nữa. Đối với Haskell, việc gọi doubleMe đối với một List mà không yêu cầu kết quả ngay lập tức thì chương trình sẽ có tính trì hoãn. Khi bạn muốn xem kết quả, thì doubleMe (1) sẽ nói với doubleMe (2) rằng nó muốn kết quả, doubleMe (2) sẽ đẩy lại cho doubleMe (3) và cái thứ ba miễn cưỡng thực thi phép tính 2*1, tức là 2. doubleMe (2) nhận lấy giá trị này và đưa số 4 cho doubleMe (1). doubleMe (1) nhận lại và báo với bạn là xs[0] = 8. Như vậy chỉ có một lần duyệt qua List và thao tác tính toán chỉ thực thi khi thực sự cần.
Statically typed
Haskell có kiểu tĩnh (statically typed). Tức là khi biên dịch, compiler sẽ hiểu được kiểu dữ liệu cho đối tượng. Nếu cố gắng cộng một int và một string với nhau, compiler sẽ báo lỗi. Khác với những ngôn ngữ bạn đã từng biết, Haskell có một hệ thống kiểu rất tốt và có khả năng suy luận kiểu (type inference). Nếu khai báo a = 5 + 4, chúng ta sẽ không cần khai báo a kiểu float. Type inference giúp cho code tổng quát hơn, (giống như Python hay JavaScript, tuy nhiên cần phân biệt rõ hai ngôn ngữ này thuộc về kiểu khai báo động).
Haskell tinh tế và ngắn gọn. Vì dùng nhiều khái niệm cấp cao, chương trình Haskell thường ngắn hơn các chương trình tương đương. Và chương trình ngắn thì dễ bảo trì hơn và ít bug hơn so với chương trình dài. Tuy nhiên đây cũng là một điểm hạn chế khiến người mới bắt đầu học Haskell khó tiếp cận.
Cần gì để bắt tay vào thực hành?
Giống như những ngôn ngữ lập trình khác, để thực hành chúng ta sẽ cần một editor, như VScode và bản phân phối Haskell (Haskell Stack). Trong bản phân phối này sẽ chứa những thứ cơ bản như compiler (GHC), package manager (Cabal), Haskell language server, …
GHC có thể nhận một file Haskell (.hs) để biên dịch, tuy vậy nó cũng có chế độ console (GHCi) cho phép code trực tiếp trên terminal như Python. Bạn có thể gọi hàm từ chương trình đã biên dịch và kết quả sẽ được hiển thị tức thì. Để phục vụ mục đích học tập thì cách này dễ và nhanh hơn nhiều so với phải biên dịch mỗi khi bạn sửa đổi rồi chạy lại. Chế độ console được khởi động bằng cách gõ vào stack ghci vào terminal. Nếu bạn đã định nghĩa một số hàm trong file có tên như là myfunctions.hs, thì thao tác biên dịch các hàm này là gõ :l myfunctions, sau đó bạn có thể gọi chúng, miễn là myfunctions.hs được đặt ở cùng thư mục nơi mà ghci được khởi động. Nếu sửa code, thì chỉ cần gõ lại :l myfunctions hoặc :r.
Chuẩn bị
Điều đầu tiên là chạy interactive mode của ghc và gọi một số hàm để chill cùng Haskell.
Configuring GHCi with the following packages:
GHCi, version 8.8.3: https://www.haskell.org/ghc/ :? for help
Loaded GHCi configuration from ...
Prelude> :l
Dấu nhắc ở đây có tên là Prelude> nhưng vì nó dài, nên ta sẽ dùng kí hiệu ghci>. Nếu bạn muốn đặt lại tên cho dấu nhắc, chỉ cần gõ vào :set prompt "ghci> ". Sau đây là một số phép toán đơn giản.
ghci> 2 + 15
17
ghci> 49 * 100
4900
ghci> 1892 - 1472
420
ghci> 5 / 2
2.5
ghci>
Giống như một số ngôn ngữ khác, ta có thể thực hiện phép tính trên một dòng và thứ tự tính toán giống như thông thường, có thể dùng cặp ngoặc đơn để làm cho thứ tự phép tính rõ ràng hơn hoặc để thay đổi thứ tự thực hiện.
ghci> (50 * 100) - 4999
1
ghci> 50 * 100 - 4999
1
ghci> 50 * (100 - 4999)
-244950
Không có gì khác biệt so với các ngôn ngữ khác. Tuy nhiên, có một lỗi dễ mắc phải ở đây là số âm. Nếu chúng ta muốn tính toán với số âm thì phải luôn kẹp giữa cặp ngoặc đơn. Ví dụ, 5 * -3 thì ghci sẽ rống lên (5 * (-3) sẽ ổn hơn). Phép toán Boolean cũng tương đối rạch ròi.
ghci> True && False
False
ghci> True && True
True
ghci> False || True
True
ghci> not False
True
ghci> not (True && True)
False
Việc kiểm tra bằng.
ghci> 5 == 5
True
ghci> 1 == 0
False
ghci> 5 /= 5
False
ghci> 5 /= 4
True
ghci> "hello" == "hello"
True
Nếu 5 + “abc” hay 5 == True thì sẽ ngay lập tức có thông báo lỗi:
* No instance for (Num [Char]) arising from a use of `+'
* In the expression: 5 + "abc"
In an equation for `it': it = 5 + "abc"
GHCi báo là “abc” không phải là số, vì vậy nó không thể cộng “abc”với 5. Nếu ta thử gõ True == 5, GHCI sẽ bảo kiểu của chúng không khớp nhau. Trong khi + chỉ làm việc được với số, thì == chỉ nhận hai thứ nào đó so sánh được với nhau (bạn không thể so sánh cam với táo). Lưu ý, bạn có thể gõ vào 5 + 4.0 vì 5 có thể là số nguyên lẫn số thực. 4.0 thì không thể làm số nguyên, vì vậy 5 sẽ được biến đổi để thích nghi.
Từ đầu đến giờ chúng ta luôn dùng các hàm. Chẳng hạn, * là một hàm nhận vào hai số rồi nhân chúng với nhau. Chúng ta gọi hàm này bằng cách kẹp nó giữa hai số. Đây được gọi là kiểu hàm trung tố. Sau này, chúng ta sẽ gặp các kiểu hàm khác là tiền tố và hậu tố. Tiền tố là hàm mà khi gọi chúng ta sẽ để tên hàm phía trước tham số khi gọi hàm, ngược lại với hậu tố.
Vì hàm tiền tố rất phổ biến (trong toán lẫn các ngôn ngữ lập trình khác) nên chúng ta sẽ mặc định các hàm luôn là kiểu tiền tố. Thường thì các tham số của ham được để trong cặp ngoặc (tham số được phân biệt bởi dấu phẩy). Trong Haskell, cặp ngoặc lẫn dấu phẩy được bỏ vì nhiều lý do mà chúng ta sẽ tìm hiểu sau. Để bắt đầu, ta sẽ thử gọi một trong số các hàm nhàm chán nhất của Haskell.
ghci> succ 8
9
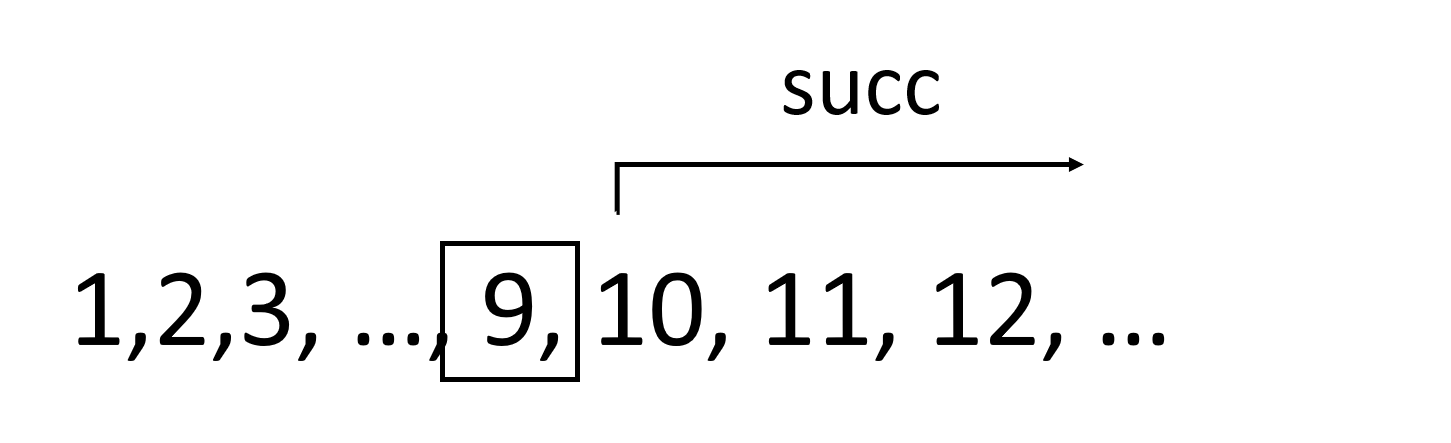
Hàm succ nhận vào thứ gì đó mà có thể trả lại thứ đứng kế tiếp nó. Như có thể thấy, ta chỉ ngăn cách tên hàm với tham số bằng một dấu cách (“ “). Việc gọi hàm với nhiều tham số cũng đơn giản.
Hàm min và max nhận vào những thứ có thể sắp xếp được. min trả lại thứ nhỏ nhất còn max trả lại thứ lớn nhất hơn.
ghci> min 9 10
9
ghci> min 3.4 3.2
3.2
ghci> max 100 101
101
Phép gọi hàm (bằng cách đặt một dấu cách ở sau nó rồi gõ vào các tham số) là phép toán có độ ưu tiên cao nhất. Có nghĩa là hai câu lệnh sau tương đương.
ghci> succ 9 + max 5 4 + 1
16
ghci> (succ 9) + (max 5 4) + 1
16
Tuy nhiên, nếu muốn tìm số đứng liền sau kết quả tích giữa các số 9 và 10, ta không thể viết succ 9 * 10 bởi nếu thế thì nó sẽ lấy số liền sau của 9 (10) rồi đem nhân với 10. Tức là 100. Ta phải viết là succ (9 * 10) mới được kết quả muốn tìm là 91. Nếu một hàm nhận hai tham số, ta cũng có thể gọi nó dưới dạng hàm trung tố bằng cách kẹp trung tố này giữa hai dấu nháy ngược. Chẳng hạn, hàm div nhận vào hai số nguyên và thực hiện phép chia nguyên giữa chúng. Viết div 92 10 ta thu được số 9. Nhưng khi ta gọi hàm như vậy, có thể vẫn gây nhầm lẫn rằng đâu là số bị chia và đâu là số chia. Vì vậy ta có thể gọi hàm này dưới dạng trung tố bằng cách viết 92 `div` 10 và nó đã rõ ràng hơn nhiều. Nhiều người trước đây quen với kiểu gọi như foo(), bar(1) hay baz(3, "haha"). Như tôi đã nói, dấu cách được dùng cho việc sử dụng hàm trong Haskell. Vì vậy những hàm đó nếu trong Haskell sẽ được viết là foo, bar 1 và baz 3 "haha".Nếu thấy một dòng code nào đó như bar (bar 3), thì nó có nghĩa là đầu tiên ta gọi hàm bar với tham số 3 để nhận được một thứ gì đó rồi mới gọi bar một lần nữa với số vừa thu được. Nếu trong C, code sẽ là bar(bar(3)). .
Viết hàm đầu tiên
Ở mục trước ta đã có một cảm nhận cơ bản về việc gọi hàm. Bây giờ, hãy thử tạo hàm! Hãy mở editor rồi gõ vào hàm sau để nhận vào một số rồi nhân đôi nó.
doubleMe x = x + x
Các hàm được định nghĩa theo cách tương tự như tên gọi. Sau tên hàm là tham số được tách rời bởi các dấu cách, sau đó là dấu = và ta sẽ định nghĩa hàm thực hiện điều gì. Lưu file này lại với tên Lab1-Intro.hs, sau đó lưu file rồi chạy ghci. Một khi đã ở trong GHCI, hãy gõ vào :l Lab1-Intro.hs. Bây giờ khi code được compile, ta có thể sử dụng hàm vừa định nghĩa.
ghci> :l Lab1-Intro.hs
[1 of 1] Compiling Main ( Lab1-Intro.hs, interpreted )
Ok, modules loaded: Main.
ghci> doubleMe 9
18
ghci> doubleMe 8.3
16.6
Hãy thử hàm phức tạp hơn là tính tổng double của hai số x và y.
doubleUs x y = x*2 + x*2
ghci> doubleUs 4 9
26
ghci> doubleUs 2.3 34.2
73.0
ghci> doubleUs 28 88 + doubleMe 123
478
Giống như thông thường, chúng ta có thể tái sử dụng các hàm. Theo cách này, ta có thể định nghĩa lại doubleUs như sau:
doubleUs x y = doubleMe x + doubleMe y
Đây là một ví dụ rất đơn giản về một dạng thông dụng mà bạn sẽ thấy xuyên suốt Haskell. Tạo ra các hàm cơ bản và hiển nhiên đúng rồi ghép chúng lại trong các hàm phức tạp hơn. Bằng cách này bạn cũng tránh được việc lặp lại. Điều gì sẽ xảy ra nếu phải đổi số 2 thành số 3. Bạn chỉ cần định nghĩa lại doubleMe thành x + x + x và vì doubleUs gọi doubleMe, nó sẽ tự động chạy đúng. Trong Haskell, hàm không nhât thiết phải có thứ tự cụ thể, vì vậy nếu bạn định nghĩa doubleMe trước rồi mới đến doubleUs, hay theo thứ tự ngược lại thì kết quả không khác gì nhau. Bây giờ ta sẽ chuẩn bị một hàm để nhân một số với 2 nhưng chỉ khi số đó nhỏ hơn hoặc bằng 100, vì những số lớn hơn 100 thì bản thân chúng đã đủ lớn rồi!
doubleSmallNumber x = if x > 100
then x
else x*2
Ngay ở đây ta biết đến lệnh if của Haskell. Điểm khác biệt giữa lệnh if trong Haskell và if trong các ngôn ngữ khác là vế else luôn bắt buộc có. Trong Haskell, với mỗi biểu thức hàm phải trả lại một thứ gì đó. Ta cũng có thể viết toàn bộ lệnh if trên một dòng nhưng tôi thấy viết kiểu trên dễ đọc hơn. Một điểm khác về câu lệnh if trong Haskell là ở chỗ nó là một biểu thức. Biểu thức về cơ bản là một đoạn code để trả lại một giá trị. 5 là một biểu thức vì nó trả lại 5, 4 + 8 là một biểu thức, x + y là một biểu thức vì nó trả lại tổng của x và y. Vì vế else là bắt buộc, nên lệnh if luôn trả lại một thứ gì đó và do đó nó là một biểu thức. Nếu ta muốn cộng thêm 1 vào kết quả được tính ra bởi hàm trên thì có thể viết phần thân hàm như sau.
doubleSmallNumber' x = (if x > 100 then x else x*2) + 1
Nếu ta bỏ cặp ngoặc tròn thì ta chỉ cộng thêm 1 vào trong trường hợp nếu x không lớn hơn 100. Lưu ý dấu ‘ ở cuối tên hàm. Dấu ‘ này không có bất kì một ý nghĩa đặc biệt nào trong cú pháp của Haskell. Nó là kí tự hợp lệ được dùng để đặt tên hàm. Tôi thường dùng ‘ để chỉ hoặc là một hàm viết theo kiểu chặt (tức là không có tính lazy) hoặc một phiên bản thứ hai của hàm hoặc biến. Vì ‘ là kí tự hợp lệ trong hàm nên ta có thể tạo một hàm như sau.
conanO'Brien = "It's a-me, Conan O'Brien!"
Có hai điều cần lưu ý ở đây. Thứ nhât là trong tên hàm ta không viết hoa chữ c vì hàm không thể bắt đầu bằng một chữ in hoa (ta sẽ biết lý do sau). Thứ hai là hàm này không nhận tham số. Khi một hàm không nhận tham số, ta thường nói nó là định nghĩa (definition) hay tên (name). Vì ta không thể thay đổi ý nghĩa của tên sau khi ta đã định nghĩa chúng.
List
Rất giống với List ngoài đời, List trong Haskell là rất hữu ích, là cấu trúc dữ liệu thường dùng nhât và nó có thể sử dụng theo nhiều cách để mô phỏng và giải quyết một loạt bài toán khác nhau. List THẬT tuyệt vời. Trong mục này ta sẽ tìm hiểu kiến thức cơ bản về List, string (là một List character) và List comperhension. Trong Haskell, List là một cấu trúc dữ liệu đồng nhất. Nó lưu trữ các phần tử có cùng kiểu, nghĩa là ta có thể có một List integer hay List character nhưng không thể có List vừa chứa integer vừa chứa character.
Lưu ý: Ta có thể dùng từ khóa let để định nghĩa một biến ngay ở trong GHCI. Viết let a = 1 trong GHCI cũng tương đương với a = 1 trong một editor.
ghci> let lostNumbers = [4,8,15,16,23,42]
ghci> lostNumbers
[4,8,15,16,23,42]
Như bạn có thể thấy, List được kí hiệu bởi cặp ngoặc vuông và các giá trị trong List được ngăn cách bởi các dấu phẩy. Nếu ta khai báo một List kiểu như [1,2,'a',3,'b','c',4], Haskell sẽ gào lên rằng các kí tự (được biểu diễn trong cặp dấu nháy đơn) không phải là số.
Lại nói về kí tự, string cũng chính là List các kí tự. "hello" chỉ là một dạng cú pháp thay cho ['h','e','l','l','o']. Bởi vì string là List nên ta cũng có thể dùng một số hàm thao tác lên List với chúng; điều này quả là tiện. Ví dụ như cộng hai List bằng toán tử ++.
ghci> [1,2,3,4] ++ [9,10,11,12]
[1,2,3,4,9,10,11,12]
ghci> "hello" ++ " " ++ "world"
"hello world"
ghci> ['w','o'] ++ ['o','t']
"woot"
Hãy cẩn thận khi liên tiếp dùng toán tử ++ đối với List dài. Khi xếp hai List cạnh nhau (ngay cả khi thêm một List đơn phần tử vào một List, chẳng hạn: [1,2,3] ++ [4]), thì ở bên trong, Haskell phải dò dọc theo toàn bộ List vế trái của ++. Điều này không đáng ngại nếu ta chỉ xử lý những List không quá lớn. Nhưng nếu đặt một thứ vào cuối một List gồm 50 triệu phần tử thì sẽ mất nhiều chút thời gian. Tuy nhiên, đặt một thứ gì đó vào đầu List bằng toán tử : (còn được gọi là toán tử cons) thì hiệu quả tức thì.
ghci> 'A':" SMALL CAT"
"A SMALL CAT"
ghci> 5:[1,2,3,4,5]
[5,1,2,3,4,5]
Lưu ý rằng toán tử : nhận một số và một List các số, hoặc một kí tự và một List kí tự, trong khi ++ nhận vào hai List. Ngay cả khi nếu bạn thêm một phần tử vào cuối List với ++, bạn phải kẹp phần tử đó giữa cặp ngoặc vuông để biến nó thành List. [1,2,3] thực ra là dạng cú pháp thay cho 1:2:3:[]. [] là một List rỗng. Nếu ta đặt 3 vào trước, nó sẽ trở thành [3]. Nếu ta đặt 2 vào trước, List mới sẽ là [2,3], và cứ như vậy. Lưu ý: [], [[]] và [[],[],[]] khác nhau. Cái đầu là một List rỗng, cái thứ hai là List bao gồm một List rỗng, còn cái thứ ba là một List bao gồm ba List rỗng. Nếu bạn muốn lấy một phần tử với chỉ số nhất định khỏi một List, hãy dùng toán tử !!.
ghci> "Steve Buscemi" !! 6
'B'
ghci> [9.4,33.2,96.2,11.2,23.25] !! 1
33.2
Nhưng nếu bạn cố gắng lấy phần tử thứ 6 khỏi một List chỉ có bốn phần tử, bạn sẽ ăn lỗi, vì vậy phải rất cẩn thận! List cũng có thể chứa List. Chúng có thể chứa các List mà bản thân List này lại chứa List bên trong …
ghci> let b = [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b ++ [[1,1,1,1]]
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3],[1,1,1,1]]
ghci> [6,6,6]:b
[[6,6,6],[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b !! 2
[1,2,2,3,4]
List bên trong List có thể dài ngắn khác nhau nhưng không thể khác kiểu nhau. Cũng như không thể có List chứa đồng thời kí tự và số, bạn không thể có một List chứa một vài List kí tự và một vài List số. List cũng có thể được so sánh với nhau nếu các thứ chứa trong đó so sánh được. Khi dùng <, <=, > và >= để so sánh các List, việc so sánh được thực hiện theo thứ tự từ vựng. Trước hết, các phần tử đầu được so sánh với nhau. Nếu chúng bằng nhau thì các phần tử thứ hai được so sánh, và cứ như vậy.
ghci> [3,2,1] > [2,1,0]
True
ghci> [3,2,1] > [2,10,100]
True
ghci> [3,4,2] > [3,4]
True
ghci> [3,4,2] > [2,4]
True
ghci> [3,4,2] == [3,4,2]
True
Ngoài ra chúng ta còn có một số hàm cơ bản thao tác lên List. head nhận vào một List rồi trả lại phần tử đầu của nó.
ghci> head [5,4,3,2,1]
5
tail nhận vào một List rồi trả lại đuôi của nó. Nói cách khác, nó chặt đầu của List đi.
ghci> tail [5,4,3,2,1]
[4,3,2,1]
last nhận vào một List rồi trả lại phần tử cuối cùng của nó.
ghci> last [5,4,3,2,1]
1
init nhận vào một List rồi trả lại tất cả mọi thứ trừ phần tử cuối cùng.
ghci> init [5,4,3,2,1]
[5,4,3,2]
Nếu ta hình dung List như một con quái vật, thì các khái niệm trên sẽ như sau.
Nhưng điều gì sẽ xảy ra nếu ta thử lấy đầu của một List rỗng?
ghci> head []
*** Exception: Prelude.head: empty List
Ồi giời ơi, kết quả tệ không ngờ được! Không có quái vật, sẽ không có cái đầu nào. Khi dùng head, tail, last và init, hãy cẩn thận tránh dùng nó với các List rỗng. Lỗi kiểu này không catch được lúc biên dịch được, cho nên điều hay là luôn phải phòng ngừa cho việc tình cờ bảo Haskell đưa cho bạn một phần tử nào đó từ một List rỗng.
length nhận vào một List rồi trả lại độ dài của nó.
ghci> length [5,4,3,2,1]
5
null là hàm kiểm tra xem List có rỗng không. Nếu có, nó sẽ trả lại True, hãy dùng hàm này thay cho việc viết xs == [] (nếu bạn có một List tên là xs).
ghci> null [1,2,3]
False
ghci> null []
True
reverse đảo ngược một List.
ghci> reverse [5,4,3,2,1]
[1,2,3,4,5]
take nhận vào một integer n và một List. Nó lấy ra n phần tử kể từ đầu List. Xem này.
ghci> take 3 [5,4,3,2,1]
[5,4,3]
ghci> take 1 [3,9,3]
[3]
ghci> take 5 [1,2]
[1,2]
ghci> take 0 [6,6,6]
[]
Lưu ý rằng nếu ta thử lấy nhiều phần tử hơn số lượng vốn có trong List, nó sẽ trả lại toàn bộ List. Nếu ta lấy 0 phần tử, ta sẽ nhận được một List rỗng.
drop làm việc theo cách ngược lại, bỏ đi từng ấy số phần tử kể từ đầu List.
ghci> drop 3 [8,4,2,1,5,6]
[1,5,6]
ghci> drop 0 [1,2,3,4]
[1,2,3,4]
ghci> drop 100 [1,2,3,4]
[]
maximum nhận vào một List các thứ có thể sắp xếp được theo cách nào đó, rồi trả lại phần tử lớn nhất. minimum trả lại phần tử nhỏ nhất.
ghci> minimum [8,4,2,1,5,6]
1
ghci> maximum [1,9,2,3,4]
9
sum nhận vào một List số rồi trả lại tổng của chúng. product nhận vào một List rồi trả lại tích của chúng.
ghci> sum [5,2,1,6,3,2,5,7]
31
ghci> product [6,2,1,2]
24
ghci> product [1,2,5,6,7,9,2,0]
0
elem nhận vào một thứ và một List rồi báo thứ đó có phải là phần tử thuộc List không. Nó thường được gọi là hàm trung tố vì nếu đọc theo kiểu đó sẽ dễ hơn.
ghci> 4 `elem` [3,4,5,6]
True
ghci> 10 `elem` [3,4,5,6]
False
Đó là một số hàm cơ bản hoạt động với List. Ta sẽ xem thêm một số hàm với List sau này.
Range
Nếu một bài toán nào đó yêu cầu chúng ta một List gồm tất cả con số từ 1 đến 20? Chắc chắn là ta có thể gõ tất cả vào nhưng hiển nhiên đó chỉ là giải pháp cục súc. Thay vào đó, chúng ta có thể dùng range. range, giống như trong Python là cách tạo List chứa loạt các phần tử đếm được. Số có thể đếm được: Một, hai, ba, bốn, v.v. Kí tự cũng có thể đếm được. Bảng chữ cái chính là một cách đếm kí tự từ A đến Z. Tên thì không thể đếm được.
Để tạo một dãy chứa các số tự nhiên từ 1 đến 20, bạn phải viết [1..20] (tương đương với [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]). Không có sự khác biệt nào giữa hai cách này ngoại trừ viết chay là việc làm hơi ngu.
ghci> [1..20]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
ghci> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
ghci> ['K'..'Z']
"KLMNOPQRSTUVWXYZ"
range còn có thể nhận vào số bước nhảy. Ví dụ như lấy số chẵn giữa 1 và 20. Hoặc cứ cách ba số thì lấy một số trong khoảng từ 1 đến 20?
ghci> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
ghci> [3,6..20]
[3,6,9,12,15,18]
Chỉ cần tách hai tham số đầu tiên bằng một dấu phẩy rồi chỉ định xem giới hạn trên bằng bao nhiêu. Tuy rằng cách này khá tiện nhưng dãy có bước nhảy không thông minh như nhiều người mong đợi. Bạn không thể viết [1,2,4,8,16..100] để có được tất cả số lũy thừa 2. Trước hết là vì bạn chỉ có thể chỉ định một bước nhảy duy nhất. Thứ hai là vì dãy không có tính chất số học sẽ rất mơ hồ nếu ta chỉ cung cấp một số ít phần tử đầu tiên. Để tạo một List với tất cả những số từ 20 về 1, bạn không thể chỉ viết [20..1], mà phải viết [20,19..1]. Ngoài ra, hãy cẩn thận khi dùng số có dấu phẩy động trong dãy! Vì chúng không chính xác hoàn toàn (theo định nghĩa) nên việc dùng chúng trong dãy có thể cho kết quả khá kì quái.
ghci> [0.1, 0.3 .. 1]
[0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]
Lời khuyên của tôi là không nên dùng chúng trong dãy. Bạn cũng có thể dùng dãy để tạo ra List vô hạn bằng việc không xác định giới hạn trên. Sau này ta sẽ tìm hiểu sâu hơn về dãy vô hạn. Hiện tại, hãy kiểm tra xem bạn làm thế nào để lấy được 24 tích số đầu tiên của 13. Tất nhiên là bạn có thể viết [13,26..24*13]. Như còn một cách khác hay hơn: take 24 [13,26..]. Vì Haskell có tính lazy, nên nó sẽ không thử tính toán ngay lập tức cả dãy vô hạn này vì việc đó sẽ không bao giờ kết thúc. Haskell sẽ đợi xem bạn muốn lấy thứ gì từ dãy vô hạn đó. Và khi biết rằng bạn chỉ muốn 24 phần tử đầu tiên, nó ngoan ngoãn nghe lời.
Một số ít các hàm tạo ra List vô hạn, ví dụ như cycle nhận vào một List rồi quay vòng nó để tạo ra một List vô hạn. Nếu bạn chỉ hiển thị kết quả, nó sẽ chạy mãi mãi nên bạn phải cắt nó ở một slot nào đó.
ghci> take 10 (cycle [1,2,3])
[1,2,3,1,2,3,1,2,3,1]
ghci> take 12 (cycle "LOL ")
"LOL LOL LOL "
repeat nhận vào một phần tử rồi tạo ra một List vô hạn chính phần tử đó. Đây là kiểu quay vòng chỉ dùng một phần tử.
ghci> take 10 (repeat 5)
[5,5,5,5,5,5,5,5,5,5]
Tuy nhiên sẽ đơn giản hơn nếu ta dùng hàm replicate, nếu muốn một số lần nào đó lặp lại một phần tử trong List. replicate 3 10 trả về [10,10,10].
List comprehension
Nếu bạn đã từng theo học môn toán, có lẽ bạn đã gặp phải set comprehension. Cách viết này thường được dùng để chỉ một tập hợp cụ thể từ tập hợp tổng quát. Một set comprehension cơ bản của tập hợp chứa 10 số tự nhiên chẵn đầu tiên là {2x|x∈N,x≤10}{2x|x∈N,x≤10}. Phần đứng trước dấu || được gọi là hàm đầu ra, xx là biến, NN là tập hợp đầu vào và x≤10x≤10 là vị ngữ. Có nghĩa là tập hợp sẽ chứa các chẵn của tất cả các số tự nhiên nào thỏa mãn vị ngữ. Nếu ta muốn viết biểu thức này trong Haskell, ta có thể viết chẳng hạn như take 10 [2,4..]. Nhưng nếu ta không muốn 10 số chẵn đầu tiên mà muốn một kiểu hàm nào đó phức tạp hơn được áp dụng cho chúng thì sao? Ta có thể dùng List comprehension. List comprehension rất giống với set comprehension. Tạm thời ta sẽ thống nhất dùng ví dụ 10 số chẵn đầu tiên. List comprehension ta có thể dùng là [x*2 | x <- [1..10]]. x được rút ra từ [1..10] và với mỗi phần tử trong [1..10] (mà ta đã “gắn” với x), ta lấy phần tử đó, chỉ x*2. Sau đây là comprehension đó khi được thực thi.
ghci> [x*2 | x <- [1..10]]
[2,4,6,8,10,12,14,16,18,20]
Như bạn đã thấy, ta thu được kết quả mong muốn. Bây giờ hãy thêm vào một điều kiện (hoặc một vị ngữ) vào comprehension đó. Vị ngữ đi sau phần gán và được phân cách với phần gắn này bởi dấu phẩy.
Chẳng hạn, ta chỉ cần các phần tử khi x*2 thì lớn hơn hoặc bằng 12.
ghci> [x*2 | x <- [1..10], x*2 >= 12]
[12,14,16,18,20]
Tuyệt, nó đã chạy đúng. Thế còn nếu muốn tất cả những số từ 50 đến 100 sao cho phần dư khi chia cho 7 thì bằng 3? Thật dễ.
ghci> [ x | x <- [50..100], x `mod` 7 == 3]
[52,59,66,73,80,87,94]
Thành công rồi! Lưu ý rằng việc dùng vị ngữ để bỏ bớt phần tử trong List còn được gọi là filtering (lọc). Ta lấy List rồi lọc chúng bằng vị ngữ. Bây giờ hãy xét ví dụ khác. Chẳng hạn, ta muốn một comprehension để thay mỗi số lẻ lớn hơn 10 bằng “BANG!” và từng số lẻ nhỏ hơn 10 bằng “BOOM!”. Nếu một số không phải số lẻ, ta sẽ vứt nó. Để cho tiện, ta sẽ đặt comprehension này vào trong một hàm để sau này dùng lại.
boomBangs xs = [ if x < 10 then "BOOM!" else "BANG!" | x <- xs, odd x]
Phần sau cùng của comprehension là vị ngữ. Hàm odd trả lại True khi gặp số lẻ và False khi gặp số chẵn. Phần tử chỉ được đứng trong List nếu tất cả các vị ngữ đều được lượng giá là True.
ghci> boomBangs [7..13]
["BOOM!","BOOM!","BANG!","BANG!"]
Ta có thể đưa vào nhiều vị ngữ khác nhau. Nếu ta muốn tất cả số từ 10 đến 20 mà không phải là 13, 15, hay 19, ta có thể viết:
ghci> [ x | x <- [10..20], x /= 13, x /= 15, x /= 19]
[10,11,12,14,16,17,18,20]
Ta không những có thể có nhiều vị ngữ trong List comprehension (một phần tử phải thỏa mãn tất cả vị ngữ mới tồn tại trong List kết quả), mà còn có thể rút từ nhiều List khác nhau. Khi rút từ nhiều List, comprehension sẽ tạo ra tất cả những tổ hợp trong các List đã cho rồi nối chúng lại bằng hàm đầu ra mà ta chỉ định. Nếu comprehension trong đó rút từ hai List có chiều dài 4 sẽ cho ra một List có chiều dài 16, nếu như ta không sử dụng filter. Giả sử ta có hai List, [2,5,10] và [8,10,11]. Nếu muốn hàm trả về tích của tất cả những tổ hợp có thể giữa các số trong List này, ta có thể viết như sau.
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]
Như mong đợi, độ dài của List mới là 9. Thế còn nếu ta muốn tất cả tích phải lớn hơn 50?
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11], x*y > 50]
[55,80,100,110]
Thế còn List comprehension trong đó kết hợp một List các tính từ và một List các động từ tiếng Anh cho vui?
ghci> let nouns = ["hobo","frog","pope"]
ghci> let adjectives = ["lazy","grouchy","scheming"]
ghci> [adjective ++ " " ++ noun | adjective <- adjectives, noun <- nouns]
["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog",
"grouchy pope","scheming hobo","scheming frog","scheming pope"]
Hãy viết một phiên bản riêng cho hàm length của riêng mình! Ta sẽ gọi nó là length'.
length' xs = sum [1 | _ <- xs]
_ có nghĩa là chúng ta cũng không quan tâm về List cho nên thay vì đặt một tên biến không bao giờ dùng đến, ta chỉ viết _. Hàm này thay thế mọi phần tử của List với 1 rồi cộng chúng lại (kết quả sẽ là chiều dài của List). Tôi xin phép nhắc lại: vì string cũng là List nên ta có thể dùng List comprehension để xử lý và sản sinh ra string. Sau đây là một hàm nhận vào một string và in ra chữ in hoa.
removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]
Khi ta thử hàm này:
ghci> removeNonUppercase "Hahaha! Ahahaha!"
"HA"
ghci> removeNonUppercase "IdontLIKEFROGS"
"ILIKEFROGS"
Vị ngữ ở đây đảm nhiệm toàn bộ công việc. Nó nói rằng kí tự được bỏ vào List mới chỉ khi nó là một phần tử của List [‘A’..’Z’].
List comprehension có thể được lồng vào nhau nếu bạn làm việc với List trong đó chứa List. Một List chứa nhiều List số. Ví dụ, xử lý List trong List mà không cần phải làm phẳng List [nghĩa là ta vẫn được giữ cấu trúc List ban đầu].
ghci> let xxs = [[1,3,5,2,3,1,2,4,5],[1,2,3,4,5,6,7,8,9],[1,2,4,2,1,6,3,1,3,2,3,6]]
ghci> [ [ x | x <- xs, even x ] | xs <- xxs]
[[2,2,4],[2,4,6,8],[2,4,2,6,2,6]]
Tuple
Ở mức độ nào đó, tuple cũng giống như List - đó là một cách lưu giữ nhiều giá trị vào một giá trị. Tuy nhiên có một vài điểm khác biệt. List số là một List chỉ chứa số. Đó là type của List này và nó không ảnh hưởng gì nếu chứa có một hay vô hạn số. Còn tuple được dùng khi bạn đã biết chắc chắn có bao nhiêu giá trị cần kết hợp lại với nhau và kiểu của tuple phụ thuộc vào số lượng phần tử (thành phần) trong nó và type của từng phần tử. Tuple được kí hiệu bằng cặp ngoặc tròn () và các component được ngăn cách bởi dấu phẩy.
Một điểm khác biệt cơ bản là tuple có thể là kết hợp nhiều kiểu dữ liệu khác nhau. Hãy hình dung cách ta biểu thị vector hai chiều trong Haskell. Một cách làm là dùng List. Có vẻ như cách này được. Vậy sẽ ra sao nếu ta muốn đưa nhiều vector vào trong một List để biểu diễn các điểm trong không gian phẳng (hai chiều)? Ta có thể viết [[1,2],[8,11],[4,5]]. Vấn đề là với cách này là ta cũng có thể lỡ may viết sai, chẳng hạn [[1,2],[8,11,5],[4,5]], điều này không gây ra lỗi cú pháp vì [8,11,5] vẫn là List số nhưng thực ra chúng đã mất ý nghĩa toán học. Còn một tuple với kích thước bằng hai (cặp) thì chính là kiểu riêng của nó. Vì vậy ta hãy dùng tuple. Thay vì bao quanh vector bởi cặp ngoặc vuông, ta dùng cặp ngoặc tròn: [(1,2),(8,11),(4,5)]. Vậy sẽ ra sao nếu ta thử tạo một hình kiểu như [(1,2),(8,11,5),(4,5)]? Ồ, ta sẽ gặp lỗi này:
* Couldn't match expected type `(a, b)' with actual type `(Integer, Integer, Integer)'.
* In the expression: (8, 11, 5)
In the expression: [(1, 2), (8, 11, 5), (4, 5)]
In an equation for `t': t = [(1, 2), (8, 11, 5), (4, 5)]
* Relevant bindings include
t :: [(a, b)] (bound at <interactive>:18:1)
Nó báo cho ta biết rằng ta đã dùng một tuple kiểu đôi và một tuple kiểu ba trong cùng List, điều này không được phép xảy ra. Bạn cũng không thể tạo List kiểu [(1,2),("One",2)] vì phần tử đầu trong List là một cặp số còn phần tử thứ hai là một cặp gồm string và số. Tuple cũng có thể được dùng để biểu diễn nhiều loại dữ liệu khác nhau. Chẳng hạn, nếu ta muốn biểu diễn tên và tuổi của một người, trong Haskell ta có thể dùng tuple ba phần tử: ("Christopher", "Walken", 55).
Như ở ví dụ này, ta thấy được tuple có thể còn chứa List. Dùng tuple khi bạn đã biết trước có bao nhiêu phần tử mà một đối tượng cần chứa. So với List thì tuple cứng nhắc hơn vì tuple kích thước khác nhau thì khác nhau, vì vậy bạn không thể viết một hàm tổng quát để thêm một phần tử vào một tuple - bạn phải viết một hàm để bổ sung vào một cặp, một hàm khác để bổ sung vào một tuple ba phần tử, một hàm khác nữa để bổ sung vào tuple bốn phần tử, …
Trong khi có List chứa một phần tử, lại không có tuple nào như vậy (thực ra khái niệm đó vô nghĩa). Tuple một phần tử chính là phần tử đó.
Cũng như List, hai tuple có thể so sánh với nhau được nếu các phần tử của chúng có thể so sánh được. Bạn chỉ không thể so sánh được hai tuple khác kích thước, nhưng hai List khác kích thước lại so sánh được. Có hai hàm có ích khi thao tác với cặp: fst nhận vào một cặp và trả về phần tử thứ nhất của nó.
ghci> fst (8,11)
8
ghci> fst ("Wow", False)
"Wow"
snd nhận vào một cặp và trả về phần tử thứ hai của nó. Thật ngạc nhiên!
ghci> snd (8,11)
11
ghci> snd ("Wow", False)
False
Lưu ý: các hàm này chỉ có tác dụng đối với cặp. Ta không dùng được với các tuple ba, tuple tứ, tuple năm, v.v. Sau này ta sẽ đề cập đến cách khác để trích thông tin từ tuple.
Một hàm rất tuyệt để tạo ra một List các cặp: zip. Nó nhận vào hai List rồi kết hợp chúng lại [thử liên tưởng đến hình ảnh phéc-mơ-tuya, cũng vì vậy mà tên hàm này là zip] bằng cách ghép các phần tử có cùng só thứ tự trong hai List thành các cặp. Đây là một hàm thực sự đơn giản nhưng có vô vàn ứng dụng. Nó đặc biệt có ích khi bạn muốn kết hợp hai List theo cách nào đó, hoặc đồng thời duyệt theo hai List. Sau đây là ví dụ sử dụng.
ghci> zip [1,2,3,4,5] [5,5,5,5,5]
[(1,5),(2,5),(3,5),(4,5),(5,5)]
ghci> zip [1 .. 5] ["one", "two", "three", "four", "five"]
[(1,"one"),(2,"two"),(3,"three"),(4,"four"),(5,"five")]
Hàm này ghép đôi các phần tử lại và tạo ra một List mới. Phần tử thứ nhất đi với phần tử thứ nhất, phần tử thứ hai đi với phần tử thứ hai, v.v. Lưu ý rằng vì cặp có thể có kiểu khác nhau, nên zip có thể nhận vào hai List có kiểu khác nhau rồi kết lại. Tuy nhiên, nếu chiều dài của các List này không bằng nhau thì sao?
ghci> zip [5,3,2,6,2,7,2,5,4,6,6] ["im","a","turtle"]
[(5,"im"),(3,"a"),(2,"turtle")]
List dài hơn sẽ được cắt bớt đi để bằng List ngắn. Vì Haskell có tính lazy, nên ta có thể zip List hữu hạn với List vô hạn:
ghci> zip [1..] ["apple", "orange", "cherry", "mango"]
[(1,"apple"),(2,"orange"),(3,"cherry"),(4,"mango")]
Sau đây là một bài toán kết hợp tuple với List comprehension: Tam giác vuông nào có các cạnh là số nguyên và các cạnh đều dài bằng hoặc ngắn hơn 10 đồng thời có chu vi bằng 24? Trước hết, ta hãy thử phát sinh tất cả tam giác với cạnh dài bằng hoặc ngắn hơn 10:
ghci> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10] ]
Ta chỉ việc rút ba số nguyên từ ba List và hàm kết quả làm nhiệm vụ kết hợp chúng thành một tuple có ba phần tử. Nếu bạn đánh giá hàm này bằng cách gõ triangles trong GHCI, bạn sẽ nhận được một List các tam giác với ba cạnh đều không dài quá 10. Tiếp theo, ta sẽ thêm vào một điều kiện để buộc chúng là tam giác vuông. Ta cũng sẽ thay đổi hàm này bằng cách tính đến cạnh b không lớn hơn cạnh huyền còn cạnh a thì không lớn hơn cạnh b.
ghci> let rightTriangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2].
Ta gần xong việc rồi. Bây giờ, chỉ cần sửa lại hàm này bằng cách nói rằng ta muốn những tam giác nào có chu vi bằng 24.
ghci> let rightTriangles' = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2, a+b+c == 24]
ghci> rightTriangles'
[(6,8,10)]
Và đó là đáp số! Trên đây là một dạng thông dụng của lập trình hàm. Bạn đem một tập các giá trị (nghiệm) khởi đầu rồi áp dụng các phép chuyển đổi cho những nghiệm đó rồi lọc đi đến khi nhận được nghiệm đúng.
Tài liệu tiếng Anh khác