Bài 10: Cấu trúc dữ liệu đệ quy và Typeclass và YesNo
Cấu trúc dữ liệu đệ quy
Như đã thấy, constructor trong kiểu dữ liệu đại số có thể chứa vài (hoặc không có) trường và mỗi trường phải là kiểu dữ liệu cụ thể nào đó. Trên quan điểm này, ta có thể tạo ra các kiểu dữ liệu mà constructor có các trường cùng kiểu với nhau. Hay ta có thể tạo ra kiểu dữ liệu có tính đệ quy, trong đó mỗi giá trị thuộc kiểu bất kỳ sẽ chứa giá trị cùng kiểu, đến lượt giá trị con thì lại chứa những giá trị khác cùng kiểu và cứ như vậy.
Hãy hình dung List sau: [5] (viết dài dòng là 5:[]). Vế trái của : có một giá trị và vế phải là List, trong trường hợp này là List rỗng. Bây giờ, List [4,5] là 4:(5:[]). Nhìn vào dấu : thứ nhất, ta thấy rằng nó có một phần tử ở vế trái và một List 5:[] ở vế phải. Tương tự với List 3:(4:(5:6:[])), hoặc 3:4:5:6:[] (vì phép toán : có tính kết phải) hoặc [3,4,5,6]. Ta có thể nói rằng List có thể là List rỗng hoặc là một phần tử nối : đến List khác (bản thân List này có thể rỗng hoặc không).
Khi thực thi:
data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
Dòng trên có thể được phiên dịch như sau: List là List rỗng hoặc là tổ hợp của head (một giá trị đơn lẻ) và một List khác. Nếu biểu diễn bằng record có lẽ sẽ dễ hiểu hơn.
data List a = Empty | Cons {
ListHead :: a,
ListTail :: List a
} deriving (Show, Read, Eq, Ord)

Bạn cũng có thể thấy lúng túng về từ khóa Cons ở đây. Cons là cách viết khác của :. Trong List, : chính là một constructor nhận vào một giá trị cụ thể và một List khác rồi trả về List mới. Nói cách khác, nó gồm hai trường, một trường có kiểu a còn trường kia có kiểu [a].
ghci> Empty
Empty
ghci> 5 `Cons` Empty
Cons 5 Empty
ghci> 4 `Cons` (5 `Cons` Empty)
Cons 4 (Cons 5 Empty)
ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty))
Cons 3 (Cons 4 (Cons 5 Empty))
Ta gọi constructor Cons theo dạng trung tố vì [] và 4 Cons (5 Cons Empty) giống 4:(5:[]).
Ta có thể định nghĩa hàm trung tố một cách tự động bằng cách đặt tên hàm bằng những kí tự đặc biệt. Ta cũng có thể làm điều tương tự với các constructor, vì chúng chỉ là hàm trả về một kiểu dữ liệu.
infixr 5 :-:
data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)

Trước hết, ta nhận thấy một cấu trúc cú pháp mới, đó là khai báo định tố. Khi ta định nghĩa hàm dưới dạng toán tử, thì ta có thể dùng khai báo đó để gán cho hàm này một kiểu định tố (nhưng không nhất thiết phải làm điều này). Định tố quy định toán tử có mức ưu tiên tính toán đến đâu và phép tính kết trái hay phải. Chẳng hạn, định tố của * là infixl 7 * và + là infixl 6 +. Điều này nghĩa là cả hai phép toán đều kết trái (4 * 3 * 2) bằng (4 * 3) * 2) nhưng * có độ ưu tiên cao hơn +, và vì vậy, 5 * 4 + 3 bằng (5 * 4) + 3.
Quay về ví dụ hiện tại, ta có thể code a :-: (List a) thay vì Cons a (List a). List mới như sau:
ghci> 3 :-: 4 :-: 5 :-: Empty
(:-:) 3 ((:-:) 4 ((:-:) 5 Empty))
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> 100 :-: a
(:-:) 100 ((:-:) 3 ((:-:) 4 ((:-:) 5 Empty)))
Khi kế thừa Show, Haskell sẽ vẫn hiển thị nó như thể constructor là hàm tiền tố, vì vậy có cặp ngoặc tròn bao quanh toán tử (nhớ rằng, 4 + 3 chính là (+) 4 3).
Ta hãy tạo một hàm để kết hai List ta vừa code lại với nhau. Với List thường, ta có toán tử ++ đảm nhiệm việc này:
infixr 5 ++
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)
Như vậy ta sẽ cướp đoạn code đó cho List ta vừa code và đặt tên hàm mới là .++.
infixr 5 .++
(.++) :: List a -> List a -> List a
Empty .++ ys = ys
(x :-: xs) .++ ys = x :-: (xs .++ ys)
Xem nó làm việc ra sao:
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> let b = 6 :-: 7 :-: Empty
ghci> a .++ b
(:-:) 3 ((:-:) 4 ((:-:) 5 ((:-:) 6 ((:-:) 7 Empty))))
Rất đẹp. Nếu muốn, ta có thể code tất cả các hàm của List thường để hoạt động với List ta vừa tạo. Lưu ý cách ta pattern matching với (x :-: xs). Cách này phát huy tác dụng vì pattern matching thực ra là match các constructor. Ta có thể match với :-: vì nó là constructor dành cho List của ta, đồng thời ta cũng có thể match với : vì nó là constructor dành cho List có sẵn. Tương tự với []. Bởi vì pattern matching (chỉ) làm việc với constructor, nên ta có thể match với tất cả những thứ như vậy, các constructor tiền tố thông thường hoặc kiểu như 8 hoặc 'a', về cơ bản là constructor với kiểu số và Char.
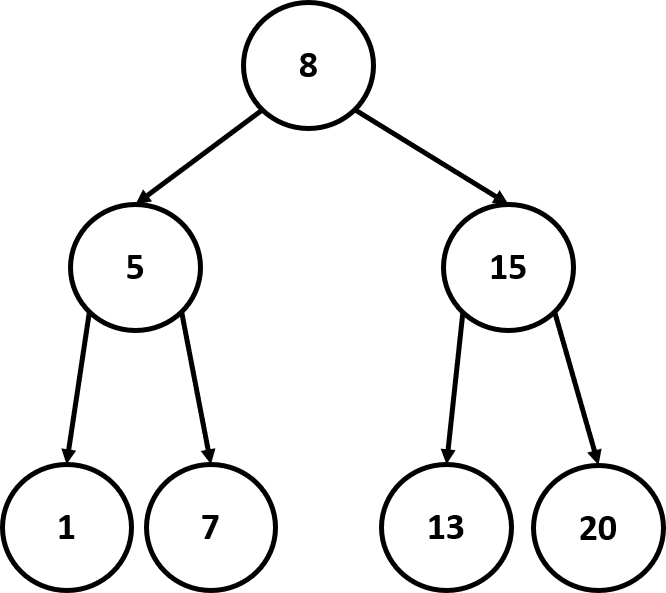
Bây giờ, hãy xem xét một cấu trúc dữ liệu đệ quy khác là cây tìm kiếm nhị phân (Binary search tree - BST). Cho những ai chưa biết: BST gồm hai node, node trái và node phải. Node trái thì có giá trị nhỏ hơn node gốc và ngược lại với node phải. Mỗi node có thể có hai node con (hoặc một hoặc không). Hệ quả là mỗi node có hai cây con. Và một điều hay về cây tìm kiếm nhị phân là toàn bộ node trên cây con bên trái sẽ nhỏ hơn node cha, chẳng hạn node cha là 5 thì sẽ nhỏ hơn 5. Vì vậy nếu ta tìm 8 có trên cây hay không, thì ta có thể bắt đầu từ gốc là 5 và vì 8 lớn hơn 5, ta đệ quy về bên phải và cứ như vậy, độ phức tạp chỉ còn là O(logN)O(logN). Cây có thể rỗng, hoặc là node chứa giá trị nào đó cùng với hai cây. Nghe thật phù hợp với một kiểu dữ liệu đại số!
data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)
Thay vì code cách thủ công, ta sẽ tạo hàm nhận vào một cây và một phần tử rồi chèn phần tử lên cây. Ta có thể làm điều này bằng cách so sánh giá trị cần chèn vào với giá trị tại gốc và nếu nó nhỏ hơn, ta sẽ đi về bên trái và ngược lại. Tương tự với node tiếp theo tới khi ta gặp cây rỗng. Một khi gặp cây rỗng, ta chỉ việc chèn node với giá trị đó vào cây rỗng.
Trong C, ta có thể dùng con trỏ để sửa đổi cây. Trong Haskell, ta không thể sửa cây, vì vậy phải tạo cây con mới mỗi lần quyết định đi bên trái hoặc phải và cuối cùng chèn phần tử trả về vào cây hoàn toán mới, vì Haskell thực sự không có con trỏ mà chỉ có giá trị. Vì vậy kiểu của hàm chèn sẽ có dạng như a -> Tree a - > Tree a. Nó nhận một phần tử và một cầy rồi trả về một cây mới có phần tử này ở trên đó. Điều này nghe có vẻ không hiệu quả nhưng tính lazy của Haskell sẽ giải quyết vấn đề này.
Sau đây là hai hàm cần code. Một là hàm tạo ra một cây đơn (cây chỉ có một nút) và hàm chèn một phần tử vào cây.
singleton :: a -> Tree a
singleton x = Node x EmptyTree EmptyTree
treeInsert :: (Ord a) => a -> Tree a -> Tree a
treeInsert x EmptyTree = singleton x
treeInsert x (Node a left right)
| x == a = Node x left right
| x < a = Node a (treeInsert x left) right
| x > a = Node a left (treeInsert x right)
Trong hàm chèn, đầu tiên là điều kiện biên, nếu gặp cây rỗng, có nghĩa là ta đã đến nơi cần đến và chèn node vào chỗ trống. Nếu không chèn vào một cây rỗng, thì ta phải kiểm tra điều gì đó. Trước hết, nếu phần tử định chèn bằng đúng phần tử ở điểm gốc cây thì trả về cây ban đầu. Nếu nó nhỏ hơn, thì trả về cây có cùng gốc cùng cây con bên phải nhưng thay cây con bên trái sẽ bị chèn. Tương tự nhưng theo chều ngược lại.
Tiếp theo, ta tạo một hàm kiểm tra xem phần tử nào đó có trên cây hay không. Trước hết, hãy định nghĩa điều kiện biên. Nếu ta cần tìm một phần tử trên cây rỗng, thì rõ ràng là không có. Được rồi. Ta thấy cách này giống với thao tác tìm kiếm trên List. Nếu ta tìm phần tử trong List rỗng, nó sẽ không có ở đó. Nếu phần tử ở điểm gốc chính là giá trị cần tìm thì quá tốt! Còn nếu không thì sao? Ta có thể lợi dụng thông tin là phần tử bên trái đều nhỏ hơn gốc. Vì vậy nếu phần tử ta cần tìm nhỏ hơn gốc thì hãy kiểm tra cây con trái. Nếu lớn hơn thì hãy kiểm tra ở cây con phải.
treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right)
| x == a = True
| x < a = treeElem x left
| x > a = treeElem x right
Hãy nghịch với cây ta vừa tạo! Thay vì code thủ công (dù ta có thể làm được), ta sẽ dùng fold để khởi tạo cây từ List. Hãy nhớ rằng, gần như mọi thao tác duyệt sẽ có thể code bằng fold! Bắt đầu với cây rỗng và rồi tiếp cận List từ bên phải và chỉ việc liên tiếp chèn những phần tử lên cây.
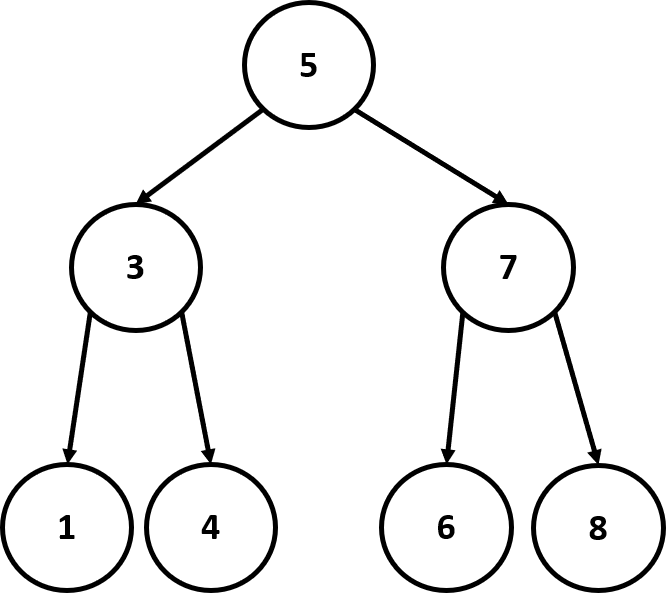
ghci> let nums = [8,6,4,1,7,3,5]
ghci> let numsTree = foldr treeInsert EmptyTree nums
ghci> numsTree
Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree))
Trong foldr, treeInsert là hàm fold (nó nhận vào một cây và một phần tử của List rồi tạo cây mới) và EmptyTree là cây tích lũy ban đầu. nums dĩ nhiên là List được fold.
Khi ta in cây ra màn hình thì kết quả tương đối khó đọc, nhưng nếu cố gắng, ta sẽ hình dung được cấu trúc của nó. Ta thấy rằng giá trị ở gốc bằng 5 và nó có 2 cây con, trong đó một có gốc bằng 3 và một có gốc bằng 7, …
ghci> 8 `treeElem` numsTree
True
ghci> 100 `treeElem` numsTree
False
ghci> 1 `treeElem` numsTree
True
ghci> 10 `treeElem` numsTree
False
Việc kiểm tra xem phần tử có thuộc cây hay không cũng diễn ra trôi chảy. Tuyệt.
Vậy như bạn có thể thấy, cấu trúc dữ liệu đại số thực sự là khái niệm mạnh trong Haskell. Ta có thể dùng chúng để tạo ra bất kì thứ gì từ Bool, Day cho đến BST và còn hơn thế nữa!
Class chứa kiểu
Đến giờ, ta đã học được một số typeclass chuẩn của Haskell, những kiểu có trong typeclass đó và cách tự động tạo ra những thể hiện bằng cách đề nghị Haskell giúp ta kế thừa. Trong mục này, ta sẽ học cách tạo nên class riêng và các thể hiện thuộc class đó.
Ôn lại về khái niệm typeclass: Typeclass (hay class chứa kiểu) giống như interface. Một typeclass định nghĩa hành vi nào đó như so sánh ngang bằng, so sánh hơn kém/thứ tự, liệt kê. Hành vi của typeclass là một số hàm nào đó hoặc chỉ là định nghĩa kiểu. Vì vậy khi ta nói kiểu là thể hiện của typeclass, ý nghĩa sâu xa là có thể dùng các hàm typeclass đã định nghĩa trên kiểu nói trên.
Typeclass trong Haskell không liên quan đến class OOP. Điều này có thể khiến nhiều người nhầm lẫn, vì vậy tôi muốn bạn quên đi tất cả về class OOP.
Chẳng hạn, typeclass Eq dành cho những thứ có thể so sánh ngang bằng (định nghĩa hàm == và /=). Nếu ta có kiểu (chẳng hạn như Car) và việc so sánh hai xe hơi bằng == là hợp pháp, Car là thể hiện của Eq.
Dưới đây là cách mà class Eq được định nghĩa trong module Prelude:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
Oa! Ở đây có kiểu cú pháp và từ khóa mới! Trước hết, class Eq a where có nghĩa là ta định nghĩa một typeclass mới tên Eq. Ở đây a là một tham số (biến) kiểu và có nghĩa là a sẽ đóng vai trò là kiểu thuộc class Eq. Nó đơn giản chỉ cần dùng một chữ thường để đại diện (có người thấy dễ hiểu hơn khi codeclass Eq equatable where, (==) :: equatable -> equatable -> Bool, …). Sau đó, ta định nghĩa vài hàm. Không cần thiết phải code cho phần thân hàm, mà ta chỉ cần khai báo kiểu cho các hàm này.
Dù sao chúng ta đã code phần thân hàm mà class Eq định nghĩa, chỉ khác là ta định nghĩa chúng dưới dạng đệ quy tương hỗ. Ta nói rằng hai thể hiện Eq bằng nhau nếu chúng không khác và chúng khác nhau nếu không bằng. Không nhất thiết phải code như vậy nhưng ta sẽ sớm thấy được ích lợi của cách code này.
Nếu ta có, chẳng hạn, class Eq a where và rồi định nghĩa một khai báo kiểu bên trong class đó như (==) :: a -> -a -> Bool, thì sau khi kiểm tra kiểu của hàm trên, nó sẽ có kiểu (Eq a) => a -> a -> Bool.
Vì vậy một khi đã có class, chúng ta chỉ có nhiều điều thú vị khi bắt đầu tạo kiểu thuộc class đó, Ví dụ kiểu sau:
data TrafficLight = Red | Yellow | Green
Nó xác định các trạng thái của đèn giao thông. Ta sẽ không kế thừa bất kì class nào, vì ta sẽ tự code một số hàm, mặc dù có thể kế thừa Eq và Show. Sau đây là cách khiến nó trở thành thể hiện của class Eq.
instance Eq TrafficLight where
Red == Red = True
Green == Green = True
Yellow == Yellow = True
_ == _ = False
Ta thực hiện điều này bằng cách dùng từ khóa instance. Như vậy, class được dùng để định nghĩa typeclass mới và instance dùng để khiến cho kiểu tự định nghĩa trở thành thể hiện của typeclass. Khi định nghĩa Eq, Eq a where, a đóng vai trò là kiểu bất kì sẽ trở thành thể hiện về sau. Ở đây, ta có thể thấy điều đó rõ hơn vì khi tạo ra một thể hiện bằng instance Eq TrafficLight where, a đã được thay thế bằng kiểu dữ liệu cụ thể.
Vì == được định nghĩa theo /= và ngược lại trong khai báo class, nên ta chỉ phải thay đổi một trong hai định nghĩa trên trong khai báo. Việc này được gọi là định nghĩa tối thiểu (minimal complete definition) cho typeclass - một số tối thiểu các hàm cần để kiểu vừa định nghĩa có hành vi giống như class. Để hoàn thành định nghĩa tối thiểu cho Eq, ta phải có một trong hai hàm == hoặc /=. Nếu Eq đơn giản được định nghĩa như sau:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
thì ta sẽ phải code cho cả hai hàm vì nếu không Haskell không biết hai hàm trên có liên hệ ra sao. Cách định nghĩa tối thiểu sẽ là: cả == lẫn /=.
Bạn có thể thấy rằng chúng ta đoạn code cho định nghĩa == là pattern matching. Vì hai ngọn đèn giao thông có thể khác nhau trong nhiều trường hợp, ta đã chỉ định những trường hợp nào thì bằng nhau và sau đó đơn giản là pattern “catch - all”, nếu không gặp ba trường hợp trên thì hai đèn sẽ khác nhau.
Đồng thời, ta hãy làm cho kiểu này trở thành thể hiện của Show. Để thỏa mãn định nghĩa tối thiểu cho Show, ta chỉ phải code ba hàm, những hàm này nhận một giá trị và biến nó thành string.
instance Show TrafficLight where
show Red = "Red light"
show Yellow = "Yellow light"
show Green = "Green light"
Một lần nữa, ta đã hoàn thành bằng cách dùng pattern matching. Hãy xem nó hoạt động ra sao:
ghci> Red == Red
True
ghci> Red == Yellow
False
ghci> Red `elem` [Red, Yellow, Green]
True
ghci> [Red, Yellow, Green]
[Red light,Yellow light,Green light]
Tuyệt. Đáng ra chỉ cần kế thừa Eq và nó cũng có hiệu quả tương tự (song vì tự học nên tôi không làm vậy). Tuy nhiên, việc kế thừa Show đã trực tiếp chuyển đổi constructor value thành string. Nếu ta muốn ngọn đèn được biểu diễn như “Red light”, ta phải tự tay khai báo.
Bạn cũng có thể tạo typeclass là con của một typeclass khác. Ví dụ về khai báo class Num (hơi dài nên tôi chỉ liệt kê phần đầu):
class (Eq a) => Num a where
...
Như đã đề cập từ trước, ta có thể chèn ràng buộc vào trong class. trường hợp trên là kiểu dữ liệu a phải là thể hiện của Eq trước khi nó trở thành thể hiện của Num. Trước khi một kiểu nào đó được coi là Num thì ta phải xác định các giá trị thuộc kiểu đó có thể so sánh bằng / khác được hay không (tính chất của typeclass Eq). Điều này hoàn toàn hợp lý.
Đó là tất cả nội dung của việc tạo typeclass con, chỉ là một ràng buộc trong khai báo class! Khi định nghĩa phần thân hàm typeclass hoặc thể hiện, ta được phép giả thiết a thuộc Eq và có thể dùng == đối với các giá trị thuộc kiểu này.
Tuy nhiên có đôi chút vấn đề với Maybe và List. Điều khiến cho Maybe trở nên khác với, chẳng hạn, TrafficLight là bản thân Maybe không phải là một kiểu cụ thể, nó là type constructor nhận vào tham số kiểu (như Char hoặc thứ gì đó) và tạo ra kiểu cụ thể (như Maybe Char). Ta hãy xét class Eq:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
Từ khai báo kiểu, ta thấy rằng a được dùng như kiểu cụ thể vì tất cả các kiểu trong hàm phải là cụ thể (nhớ rằng bạn không thể có hàm kiểu a -> Maybe nhưng bạn có thể có hàm a -> Maybe a hoặc Maybe Int -> Maybe String). Điều này lý giải tại sao ta không thể có:
instance Eq Maybe where
Vì a phải là kiểu cụ thể nhưng Maybe có thể không phải cụ thể. Nó là type constructor nhận vào một tham số và tạo ra kiểu cụ thể. Sẽ rất nhàm chán nếu đặt trường hợp ta phải xử trí với instance Eq (Maybe Int) where, instance Eq (Maybe Char) where, … lặp lại nhiều lần. Vì vậy ta có giải pháp sau:
instance Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
Điều này nói rằng ta muốn tất cả những kiểu có dạng Maybe something trở thành thể hiện của Eq. Thực chất, ta có thể code Maybe something nhưng chọn một chữ cái để hợp với phong cách Haskell. Ở đây, (Maybe m) ngang với a trong class Eq a where. Dù Maybe không phải là một kiểu cụ thể, nhưng Maybe m thì đúng vậy. Bằng cách chỉ định tham số kiểu (m, chữ thường), ta nói rằng tất cả những kiểu dạng Maybe m, trong đó m là kiểu bất kì, trở thành thể hiện của Eq. Tuy vậy, còn một vấn đề với cách làm trên, ta đã dùng == đối với Maybe mà không ràng buộc thứ chứa trong Maybe. Ta phải sửa khai báo lại như sau:
instance (Eq m) => Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
Với khai báo này, ta muốn tất cả những kiểu có dạng Maybe m thuộc về class Eq, nhưng chỉ những kiểu nào thuộc Eq. Đây là cách mà Haskell kế thừa.
Trong đa số trường hợp, ràng buộc trong khai báo typeclass được dùng để một typeclass trở thành con của một typeclass khác và ràng buộc được dùng để thể hiện yêu cầu về nội dung một kiểu nào đó. Chẳng hạn, ở đây ta yêu cầu nội dung của Maybe cũng phải thuộc về class Eq.
Khi tạo thể hiện, nếu có kiểu cụ thể trong khai báo (như a trong a -> a -> Bool), bạn phải cung cấp tham số kiểu và thêm cặp ngoặc tròn để thu được một kiểu cụ thể.
Hãy tính đến thể hiện thuộc kiểu mà bạn đang cố gắng thay thế tham số trong khai báo class. a trong class Eq a where sẽ được thay thế bằng một kiểu cụ thể vì vậy cố gắng hình dung kiểu đang xét vào cùng khai báo kiểu. (==) :: Maybe -> Maybe -> Bool không hợp lý lắm nhưng (==) :: (Eq m) => Maybe m -> Maybe m -> Bool thì được. Tuy nhiên đây chỉ là điều cần tính đến, vì == sẽ luôn có kiểu (==) :: (Eq a) => a -> a -> Bool, bất kể các thể hiện là gì.
Còn một điều nữa cần kiểm tra! Nếu bạn muốn biết các thể hiện của một class là gì, chỉ cần gõ :info YourTypeClass vào GHCI. Vì vậy, việc gõ :info Num sẽ cho thấy những hàm mà typeclass đã định nghĩa và nó sẽ cho bạn List các kiểu trong class. :info cũng hoạt động với kiểu và type constructor. Nếu bạn gõ vào :info Maybe, GHCI sẽ cho bạn thấy tất cả những class mà Maybe là thể hiện trong đó. Ngoài ra, :info còn cho bạn thấy khai báo kiểu của hàm. Tôi nghĩ nó rất hay.
Yes / No
Trong JavaScript, chúng ta có thể đặt bất kì thứ gì vào trong if. Chẳng hạn,
if (0) alert("YEAH!") else alert("NO!")`
if ("") alert ("YEAH!") else alert("NO!")
if (false) alert("YEAH") else alert("NO!)
và chúng đều xuất ra thông báo NO!. Còn:
if ("WHAT") alert ("YEAH") else alert("NO!")
Sẽ xuất thông báo YEAH! vì JavaScript coi String không rỗng sẽ là true.
Dù việc chỉ dùng Bool trong ngữ cảnh cần biểu thức logic sẽ tốt hơn đối với Haskell, ta hãy thử code theo kiểu JavaScript. Để cho vui thôi! Ta hãy bắt đầu bằng một khai báo class.
class YesNo a where
yesno :: a -> Bool
Thật đơn giản. Class YesNo chỉ định nghĩa một hàm. Hàm này nhận vào giá trị thuộc kiểu có khái niệm yes / no. Có thể nhận thấy rằng, từ cách dùng a trong hàm, thì a phải là kiểu cụ thể.
Tiếp theo, ta định nghĩa vài thể hiện. Đối với các con số, ta sẽ giả sử rằng (như ở JavaScript) một số khác 0 bất kì là đúng và 0 là sai.
instance YesNo Int where
yesno 0 = False
yesno _ = True
List rỗng là False, còn List không rỗng là True.
instance YesNo [a] where
yesno [] = False
yesno _ = True
Lưu ý cách ta chỉ đặt tham số kiểu a vào để làm cho List trở thành kiểu cụ thể, mặc dù ta không giả định gì về kiểu của các phần tử trong List. Còn gì nữa nhỉ, hừm, tôi biết rồi, bản thân Bool có giá trị đúng - sai và điều này hiển nhiên.
instance YesNo Bool where
yesno = id
id là gì? Đó là hàm trong thư viện chuẩn, hàm này nhận vào tham số rồi trả về chính thứ đó.
Maybe a cũng có thể là một thể hiện.
instance YesNo (Maybe a) where
yesno (Just _) = True
yesno Nothing = False
Ta không cần ràng buộc về class vì ta không giả thiết gì về nội dung của Maybe. Ta chỉ nói rằng True nếu nó là Just và False nếu nó là Nothing. Ta vẫn sẽ phải code rõ Maybe a thay vì chỉ Maybe vì nếu bạn thử nghĩ xem, Maybe -> Bool không thể tồn tại (vì Maybe không phải là kiểu cụ thể), còn Maybe a -> Bool thì lại được. Dù vậy thì vẫn rất hay bởi bây giờ, bất kì kiểu nào có dạng Maybe something đều thuộc về YesNo và không phụ thuộc vào something là cái gì. Trước đây, ta định nghĩa Tree a biểu diễn cây tìm kiếm nhị phân. Ta có thể nói rằng cây rỗng là False và bất kì cây nào không rỗng đều true.
instance YesNo (Tree a) where
yesno EmptyTree = False
yesno _ = True
Liệu đèn giao thông có giá trị đúng sai không? Được chứ. Nếu đèn đỏ, bạn dừng. Nếu đèn xanh, bạn đi. Còn đèn vàng? À, với tôi thì thường là phóng tiếp.
instance YesNo TrafficLight where
yesno Red = False
yesno _ = True
Được rồi, hãy nghịch chơi!
ghci> yesno $ length []
False
ghci> yesno "haha"
True
ghci> yesno ""
False
ghci> yesno $ Just 0
True
ghci> yesno True
True
ghci> yesno EmptyTree
False
ghci> yesno []
False
ghci> yesno [0,0,0]
True
ghci> :t yesno
yesno :: (YesNo a) => a -> Bool
Được rồi, nó đã hoạt động! Ta hãy code một hàm phỏng if, nhưng hoạt động với các giá trị YesNo.
yesnoIf :: (YesNo y) => y -> a -> a -> a
yesnoIf yesnoVal yesResult noResult = if yesno yesnoVal then yesResult else noResult
Khá là dễ. Nó nhận vào một giá trị kiểu Yes / No và hai thứ. Nếu cái Yes / No kia là đúng thì nó trả về cái thứ nhất, còn không thì trả về cái thứ hai.
ghci> yesnoIf [] "YEAH!" "NO!"
"NO!"
ghci> yesnoIf [2,3,4] "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf True "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf (Just 500) "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf Nothing "YEAH!" "NO!"
"NO!"