Bài 04: Đệ quy
Thuật toán được dùng phổ biến trong Haskell.
Đệ quy là gì?
Đệ quy là một khái niệm cơ bản trong thế giới lập trình. Tuy ý tưởng về đệ quy vẫn không đổi trong Haskell, tuy nhiên với Haskell chúng ta sẽ có cảm giác đệ quy được áp dụng một cách mượt mà, uyển chuyển hơn.
Tôi xin được nhắc lại, đệ quy là một cách định nghĩa hàm trong chính bản thân nó. Nhiều định nghĩa trong toán học được trình bày tinh tế dưới dạng đệ quy, chẳng hạn dãy Fibonacci, ta định nghĩa hai phần tử đầu tiên F(0)\=0F(0)\=0 và F(1)\=1F(1)\=1, nghĩa là các số Fibonacci thứ 0 và thứ 1 lần lượt bằng 0 và 1, còn với mọi số tự nhiên khác thì số Fibonacci sẽ bằng tổng của hai số Fibonacci liền trước (F(n)\=F(n−1)+F(n−2)F(n)\=F(n−1)+F(n−2)). Trình bày một cách dài dòng, F(3)\=F(2)+F(1)F(3)\=F(2)+F(1) và tương tự với những số Fibonacci tiếp theo. Việc chúng ta định nghĩa hai phần tử không liên quan đến đệ quy (như F(0)F(0) và F(1)F(1)) còn được gọi là điều kiện biên (edge / boundary condition), điều kiện biên không được phép thiếu vì nó giúp thuật toán đạt được trạng thái dừng (idle state). Ví dụ, nếu không định nghĩa F(0) và F(1), thì F(-1) bằng F(-2) + F(-3) và máy tính sẽ đi đời trước khi đưa ra đáp án.
Tôi xin nhắc lại ý tưởng cốt lõi trong Haskell là khi chúng ta sử dụng nó, chúng ta giải quyết bài toán bằng cách định nghĩa đối tượng là gì chứ không phải định nghĩa bằng cách nào để đạt được nó. Đây là lý do tại sao không có while hoặc for, và đệ quy là công cụ thực hiện chức năng tương đương.
Maximum
Như chúng ta đã biết, hàm maximum nhận vào List các phần tử có thể sắp xếp (lớp Ord) rồi trả về phần tử lớn nhất trong đó. Nếu không dùng đệ quy, chúng ta có thể tạo một biến để khởi tạo và lần lượt so sánh xem phần tử đầu tiên là phần tử lớn nhất, nếu phần tử được so sánh lớn hơn giá trị lớn nhất hiện có, bạn sẽ thay thế nó bằng phần tử mới ấy. Tuy đó là cách nhanh nhất, nhưng tôi vẫn thấy nó quá cục súc, dài dòng.
Nếu sử dụng đệ quy, trước hết ta định nghĩa điều kiện biên: giá trị lớn nhất của List một phần tử là chính phần tử đó. Tiếp theo, giá trị lớn nhất của List là head nếu như phần tử head này lớn hơn giá trị lớn nhất của tail.
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty List"
maximum' [x] = x
maximum' (x:xs)
| x > maxTail = x
| otherwise = maxTail
where maxTail = maximum' xs
Quả thật pattern matching rất hợp với đệ quy! Đa số các ngôn ngữ phải dùng if else để kiểm tra điều kiện biên. Ở đây, pattern matching giúp code ngắn gọn và dễ đọc hơn rất nhiều. Điều kiện thứ nhất là nếu List rỗng, chương trình sẽ crash, điều kiện thứ hai là nếu List chỉ có một phần tử, hãy trả lại phần tử đó. Pattern thứ ba tách List thành head, taa gắn where để định nghĩa maxTail là phần tử lớn nhất của phần còn lại List. Sau đó ta kiểm tra xem liệu phần tử đầu có lớn hơn phần còn lại của List hay không. Nếu có, ta trả về head. Nếu không, ta trả về phần tử lớn nhất của tail.
Ví dụ [3,5,1].

Nếu chúng ta kết hợp với hàm có sẵn (max :: [Ord a] => a -> a -> a), code còn tinh tế hơn, đây là một ví dụ về việc kết hợp các hàm nhỏ lại với nhau:
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty List"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)
Nếu diễn đạt định nghĩa trên bằng lời: phần tử lớn nhất trong List thì bằng phần tử lớn hơn giữa phần tử đầu và phần tử lớn nhất trong phần còn lại của List. Thật thanh lịch!
Replicate
Đầu tiên, hàm replicate. replicate nhận vào một phần tử kk kiểu Int và một phần tử xx rồi trả lại List gồm phần tử đó được lặp lại nhiều lần. Chẳng hạn, replicate 3 5 trả về [5,5,5]. Điều kiện biên là nếu k≤0k≤0 thì trả về [].
replicate':: (Integral a) => a -> b -> [b]
replicate' k x
| k <= 0 = []
| otherwise = [x] ++ replicate1 (k - 1) x
Ở đây ta đã dùng guard vì cần kiểm tra điều kiện boolean. Nếu k≤0k≤0, trả về List rỗng. Ngược lại thì trả về List có x là head cùng tail là List chứa x lặp lại k−1k−1 lần. Nếu n−1\=0n−1\=0 sẽ chương trình sẽ đạt được trạng thái dừng.
Take
Tiếp theo, hàm take. Hàm này lấy ra một số lượng các phần tử trong List. Chẳng hạn, take 3 [5,4,3,2,1] trả về [5,4,3]. Nếu ta lấy ra 0, hoặc ít hơn, chương trình trả về List rỗng. Mặt khác, nếu thử lấy bất kì thứ gì từ List rỗng, ta cũng chỉ lấy được List rỗng. Lưu ý rằng có hai điều kiện biên như vậy.
take':: (Integral a) => a -> [b] -> [b]
take' k _
| k <= 0 = []
take' _ [] = []
take' k (x:xs) = x : take' (k -1) xs
Pattern thứ nhất quy định nếu muốn lấy ra k(k≤0)k(k≤0) phần tử, thì ta nhận được List rỗng. Lưu ý rằng guard không có otherwise. để trường hợp k>0k>0 thì nó rơi xuống pattern tiếp theo. Pattern thứ hai định nghĩa nếu ta yêu cầu thứ gì đó từ List rỗng, ta nhận được List rỗng. Pattern thứ ba chia List thành head và tail, List trả về là head kết với k−1k−1 phần tử ở tail.
Reverse
Đây là hàm đảo ngược List, nếu từng học các ngôn ngữ lập trình khác, chắc chắn bạn đã làm nhiều bài tập về chúng. Đầu tiên, hãy hình dung ra điều kiện biên, List rỗng đảo ngược thì bằng chính List rỗng. Về phần còn lại, ta vẫn chia List thành head và tail, reverse List sẽ bằng reverse tail kết với head.
reserve' :: [a] -> [a]
reserve' [] = []
reserve' (x:xs) = (reserve' xs) ++ [x]
Repeat
Vì Haskell cho phép dùng List vô hạn nên đệ quy không nhất thiết phải có điều kiện biên. Nhưng nếu không có, nó sẽ không ngừng tuồn ra giá trị, hoặc tạo một cấu trúc dữ liệu vô hạn, như List vô hạn. Dù vậy, điều hay ở List vô hạn là ta có thể cắt chúng ở slot ta muốn. Ví dụ như hàm repeat nhận vào một phần tử rồi trả lại List vô hạn phần tử đó. Một cách viết hàm này theo dạng đệ quy rất đơn giản, xem nhé.
repeat' :: a -> [a]
repeat' x = x:repeat' x
Khi gọi repeat 3, ta sẽ thu được List bắt đầu bằng số 3 và tiếp theo là phần đuôi gồm vô hạn các số 3. Vì vậy, repeat 3 sẽ được ước lượng thành 3:repeat 3, vốn lại bằng 3:(3:repeat 3), bằng 3:(3:(3:repeat 3)), v.v. repeat 3 sẽ không bao giờ ngừng được ước lượng, nhưng take 5 (repeat 3) sẽ cho ta List có năm con số 3. Như vậy cũng giống như viết replicate 5 3.
Zip
zip nhận vào hai List và đan chúng với nhau. zip [1,2,3] [2,3] trả về [(1,2),(2,3)], vì nó cắt bớt List dài để vừa với List ngắn. Thế nếu ta zip List với List rỗng ta sẽ nhận được List rỗng. Đó cũng chính là điều kiện biên. Tuy vậy, zip nhận hai List làm đối số, cho nên sẽ có hai điều kiện biên.
zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys
Pattern thứ ba phát biểu rằng hai List zip với nhau thì bằng việc nén 2 phần tử đầu vào 1 tuple rồi xử lý phần đuôi. Việc zip [1,2,3] và [‘a’,’b’] sẽ dẫn đến trường hợp cuối cùng phải zip [3] với []. Điều kiện biên xuất hiện và do đó kết quả là (1,’a’):(2,’b’):[], hay [(1,’a’),(2,’b’)].
Elem
Ta hãy tự code thêm một hàm đã có trong thư viện chuẩn - hàm elem. Nó nhận vào một phần tử aa và List rồi search phần tử đó trong List xem thử có hay không. Điều kiện biên là nếu tìm aa trong List rỗng thì hiển nhiên kết quả là False. Ta biết rằng List rỗng thì không chứa phần tử nào, vì vậy nó không chứa phần tử ta cần tìm.
elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
| a == x = True
| otherwise = a `elem'` xs
Khá đơn giản. Nếu head không phải là phần tử đang cần thì ta kiểm tra tail.
Sort
Ai đã từng học qua một lớp Cấu trúc dữ liệu và giải thuật đều biết rằng bài toán tìm kiếm (hay hàm elem) phía trên là một bài toán cơ bản trong rất nhiều thuật toán khác. Tuy nhiên hàm elem nếu thực hiện trên List không được sắp xếp trước đó (tăng hoặc giảm dần) thì sẽ có độ phức tạp O(N)O(N), ngược lại, nếu sắp xếp trước chúng ta có thể giảm xuống (Olog2N)(Olog2N) (tìm kiếm bằng hàm binary search thay cho elem). Nên nhớ răng trong thực tế thì đa số bài toán sẽ có số lượng truy vấn search hơn nhiều so với sort, chung quy lại thì cách thứ hai vẫn tối ưu hơn.
Do đó, trong phần này ta sẽ tìm hiểu một thuật toán có độ phức tạp thấp nhất trong các thuật toán sắp xếp là QuickSort (OlogN)(OlogN).
Quicksort khi viết bằng một số ngôn ngữ quả thật là một thảm họa, vì nó chiếm tới ít nhất là 10 dòng code, Haskell lại ngắn và thanh lịch hơn nhiều, do đó nếu sau này bạn đọc đến các tutorial khác, Quicksort có lẽ thường xuyên là “sản phẩm mẫu” cho Haskell.
Điều điều kiện biên? Quá dễ, nếu List rỗng thì sau khi sắp xếp vẫn là List rỗng. Và bây giờ là thuật toán chính: List được sắp xếp là List mà trong đó tất cả những giá trị nhỏ hơn (hoặc bằng) head của List thì được xếp lên trước (bản thân những giá trị này đã được sắp xếp), rồi đến head trong List gốc, theo sau là những phần tử lớn hơn head (bản thân chúng cũng được sắp xếp). Lưu ý rằng trong định nghĩa trên, chúng ta đã hai lần nhắc đến “được sắp xếp”, vì vậy có thể ta phải gọi đệ quy hai lần! Cũng lưu ý rằng để định nghĩa hàm ta dùng từ “là”, không phải “làm thứ này”, rồi “làm thứ kia”, … Đó chính là vẻ đẹp của lập trình hàm! Bây giờ, hơi nâng cao một chút, tôi sẽ dùng List comprehension để code ngắn gọn nhất có thể. Hãy bắt tay vào định nghĩa hàm này.
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
let smallerSorted = quicksort [a | a <- xs, a <= x]
biggerSorted = quicksort [a | a <- xs, a > x]
in smallerSorted ++ [x] ++ biggerSorted
Ta hãy chạy thử nó cho một trường hợp nhỏ để xem liệu có đúng không.
ghci> quicksort [10,2,5,3,3]
[2,3,3,5,10]
ghci> quicksort "vu tuan hai"
"aahintuuv"
Sau đây là minh họa:
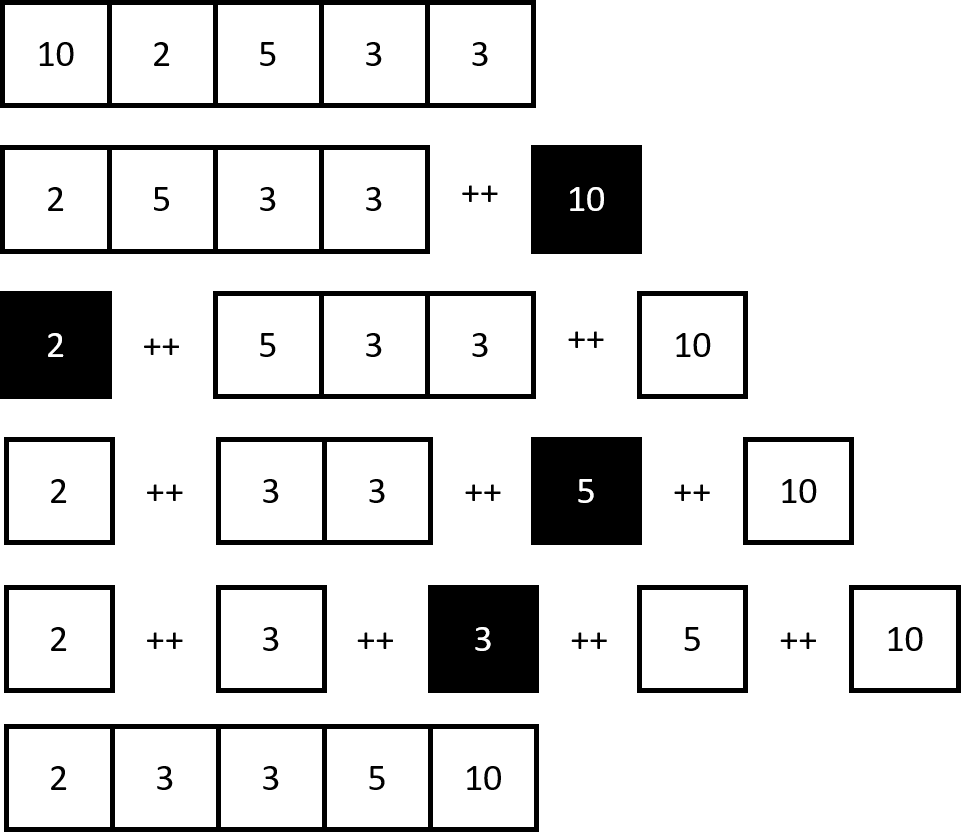
Trong quicksort, phần tử được đặt làm mốc để so sánh với tất cả các phần tử chưa sắp xếp còn lại được gọi là “pivot”, thường thì pivot là phần tử trung tâm, nhưng ví dụ trên tôi chọn phần tử đầu vì cú pháp Haskell cho phép lấy head khá dễ.
Đệ quy hóa
Khi đọc đến đây, có thể bạn đã cảm nhận tư duy của những bài trên có gì đó giống nhau, đầu tiên là điều kiện biên, sau đó định nghĩa việc gì đó giữa một phần tử và phần còn lại, bất kể đó là List, tree, hay một cấu trúc dữ liệu nào khác. Tổng là head cộng với tổng tail. Tích của List là head với tích tail. Chiều dài List bằng 1 cộng với chiều dài tail. Vân vân và vân vân …
Thông thường điều kiện biên là tình huống nào đó mà đệ quy trở nên vô nghĩa. Với List là List rỗng. Với tree thì là một node mà không có nhánh con (lá). Mỗi cấu trúc dữ liệu lại có một kiểu khác nhau.
Có đôi chút khác biệt khi bạn phải xử lý những con số bằng đệ quy. Ý tưởng cơ bản là chúng ta phải xử lý một số xx nào đó với biến thể của xx này. Ví dụ như hàm factorial là tích của một xx và giai thừa của x−1x−1. Điều kiện biên của hàm factorial là x\=0x\=0 vì giai thừa chỉ được định nghĩa trên x≥0x≥0, ta gọi x\=0x\=0 là phần tử trung hòa. Trong phép nhân, phần tử trung hòa bằng 1 vì bất cứ số gì nhân với 1 cũng nhận được chính số đó. Khi làm việc với List, ta định nghĩa tổng của List rỗng bằng 0 vì 0 chính là phần tử trung hòa trong phép cộng.
Kết luận, khi áp dụng đệ quy để giải một bài toán, bạn hãy cố hình dung xem khi nào đệ quy vô nghĩa và liệu đó có phải là điều kiện biên hay không. Hãy nghĩ về các phần tử trung hòa!